Доверительный интеграл для оценки математического ожидания при известном ${\mathbf \sigma }$
Для начала напомним следующее определение:
Доверительный интервал -- интервал $(Q^*-\delta ,Q^*+\delta )$, который покрывает неизвестную величину $Q$ c надежностью $\gamma $.
Будем рассматривать следующую ситуацию. Пусть варианты генеральной совокупности имеет нормальное распределение с математическим ожиданием $a$ и среднем квадратическим отклонением $\sigma $. Выборочное среднее в данном случае будет рассматриваться как случайная величина. Когда величина $X$ распределена нормально, выборочное среднее будет также иметь нормальное распределение с параметрами
Найдем доверительный интервал, который покрывает величину $a$ с надежностью $\gamma $.
Для этого нам необходимо, чтобы выполнялось равенство
Из нее получим
Отсюда мы можем легко найти $t$ по таблицы значений функции $Ф\left(t\right)$ и, как следствие, найти $\delta $.
Напомним таблицу значений функции $Ф\left(t\right)$:
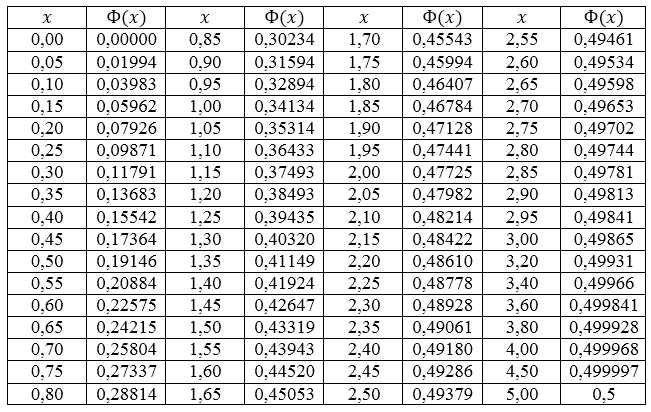
Рисунок 1. Таблица значений функции $Ф\left(t\right).$
Доверительный интеграл для оценки математического ожидания при неизвестном ${\mathbf \sigma }$
В этом случае мы будем пользоваться значением исправленной дисперсии $S^2$. Заменяя в выше выведенной формуле $\sigma $ на $S$, получим:
Пример задач на нахождение доверительного интервала
Пусть величина $X$ имеет нормальное распределение с дисперсией $\sigma =4$. Пусть объем выборки $n=64$, а надежность равна $\gamma =0,95$. Найти доверительный интервал для оценки математического ожидания данного распределения.
Решение:
Нам необходимо найти интервал ($\overline{x}-\delta ,\overline{x}+\delta )$.
Как мы видели выше
\[\delta =\frac{\sigma t}{\sqrt{n}}=\frac{4t}{\sqrt{64}}=\frac{\ t}{2}\]Параметр $t$ найдем из формулы
\[2Ф\left(t\right)=\gamma \]Откуда
\[Ф\left(t\right)=\frac{\gamma }{2}=\frac{0,95}{2}=0,475\]Из таблицы 1 получаем, что $t=1,96$.
Получаем:
\[\delta =\frac{1,96}{2}=0,98\]Ответ: ($\overline{x}-0,98,\overline{x}+0,98)$.
Пусть выборка имеет точность $\delta =0,6$ и надежность $\gamma =0,95$. При этом величина $X$ имеет нормальное распределение с $\sigma =2,4$. Найти минимальный объем выборки.
Решение.
Из формулы $\delta =\frac{\sigma t}{\sqrt{n}}$, имеем
\[n={\left(\frac{\sigma t}{\delta }\right)}^2\]Как известно, $Ф\left(t\right)=\frac{\gamma }{2}=0,475.$ Тогда из таблицы 1, получаем, что $t=1,96$.
Итого:
\[n={\left(\frac{\sigma t}{\delta }\right)}^2={\left(\frac{4,704}{0,6}\right)}^2\approx 62\]Ответ: 62.












