Распределения в математической статистике характеризуется многими статистическими параметрами. Оценка неизвестных параметров распределения на основе различных данных выборки позволяет построить распределения случайной величины.
Найти статистическую оценку неизвестного параметра распределения -- найти функцию от наблюдаемых случайных величин, которая даст приближенное значение оцениваемого параметра.
Статистические оценки можно разделить на несмещенные, смещенные, эффективные и состоятельные.
Несмещенная оценка -- статистическая оценка $Q^*$, которая при любом значении объема выборки, имеет математическое ожидание, равное оцениваемому параметру, то есть
\[M\left(Q^*\right)=Q\]Смещенная оценка -- статистическая оценка $Q^*$, которая при любом значении объема выборки, имеет математическое ожидание, не равное оцениваемому параметру, то есть
\[M\left(Q^*\right)\ne Q\]Эффективная оценка -- статистическая оценка, которая имеет наименьшее возможное значение дисперсии при заданном объеме выборки.
Состоятельная оценка -- статистическая оценка, при которой при объеме выборки, стремящейся к бесконечности, стремится по вероятности к оцениваемому параметру $Q.$
Состоятельная оценка -- статистическая оценка, при которой при объеме выборки, стремящейся к бесконечности, дисперсия несмещенной оценки стремится к нулю.
Генеральная и выборочная средние
Генеральная средняя -- среднее арифметическое значений вариант генеральной совокупности.
Выборочная средняя -- среднее арифметическое значений вариант выборочной совокупности.
Величины генерального и выборочного среднего можно найти по следующим формулам:
- Если значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$, то
- Если значения вариант $x_1,\ x_2,\dots ,x_k$ различны, то
С этим понятием связано такое понятие как отклонение от средней. Данная величина находится по следующей формуле:
Среднее отклонение обладает следующими свойствами:
-
$\sum{n_i\left(x_i-\overline{x}\right)=0}$
-
Среднее значение отклонения равно нулю.
Генеральная, выборочная и исправленная дисперсии
Еще одними из основных параметров является понятие генеральной и выборочной дисперсии:
Генеральная дисперсия:
Выборочная дисперсия:
С этими понятия связаны также генеральная и выборочная средние квадратические отклонения:
В качестве оценки генеральной дисперсии вводится понятие исправленной дисперсии:
Также вводится понятие исправленного стандартного отклонения:
Пример решения задачи
Генеральная совокупность задана следующей таблицей распределения:

Рисунок 1.
Найдем для нее генеральное среднее, генеральную дисперсию, генеральное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Решение:
Для решения этой задачи для начала сделаем расчетную таблицу:
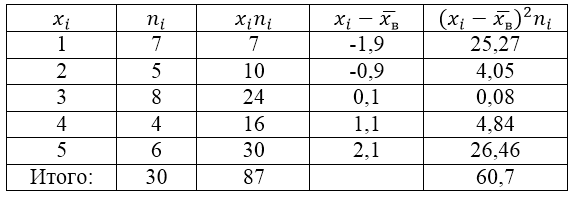
Рисунок 2.
Величина $\overline{x_в}$ (среднее выборочное) находится по формуле:
\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}\]То есть
\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}=\frac{87}{30}=2,9\]Найдем генеральную дисперсию по формуле:
\[D_в=\frac{\sum\limits^k_{i=1}{{{(x}_i-\overline{x_в})}^2n_i}}{n}=\frac{60,7}{30}=2,023\]Генеральное среднее квадратическое отклонение:
\[{\sigma }_в=\sqrt{D_в}\approx 1,42\]Исправленная дисперсия:
\[{S^2=\frac{n}{n-1}D}_в=\frac{30}{29}\cdot 2,023\approx 2,09\]Исправленное среднее квадратическое отклонение:
\[S=\sqrt{S^2}\approx 1,45\]











