Предварительные сведения
Любой треугольник имеет 6 элементов: три стороны и три угла. Рассмотрим произвольный треугольник $ABC$. Обозначим $AB=c,\ BC=a,\ AC=b$ (рис. 1).
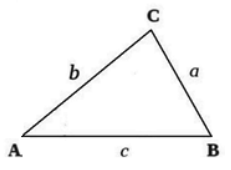
Рисунок 1. Треугольник
Решить треугольник - значит найти все его шесть элементов по трем данным элементам, определяющим треугольник.
Примеры задач на решение треугольников
Из определения мы видим, что если в треугольнике даны три каких-либо элемента треугольника, то его можно разрешить, то есть найти остальные три элемента этого треугольника. Будем рассматривать решение треугольника на примерах задач.
Пусть нам даны две стороны $a\ и\ b$ и угол $C$. Найти сторону $c$ и углы $A\ и\ B$.
Решение.
Найдем сначала третью сторону по теореме косинусов:
\[c^2=a^2+b^2-2abcosC\] \[c=\sqrt{a^2+b^2-2abcosC}\]Используя вновь теорему косинусов, имеем:
\[a^2=c^2+b^2-2cbcosA\] \[2cbcosA=c^2+b^2-a^2\] \[cosA=\frac{c^2+b^2-a^2}{2bc}\] \[\angle A=arc\ cos\left(\frac{c^2+b^2-a^2}{2bc}\right)\]По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C={180}^0\] \[\angle B={180}^0-\angle A-\angle C\]Ответ: $c=\sqrt{a^2+b^2-2abcosC},\ \ $
\[\angle A=arc\ cos\left(\frac{c^2+b^2-a^2}{2bc}\right),\angle B={180}^0-\angle A-\angle C.\]Пусть нам дана одна сторона $a$ и два угла: $B$ и $C$. Найти стороны $b$ и $c$ и угол $A$.
Решение.
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C={180}^0\] \[\angle A={180}^0-\angle B-\angle C\]По теореме синусов, имеем:
\[\frac{b}{a}=\frac{sinB}{sinA}\Rightarrow b=a\frac{sinB}{sinA}\] \[\frac{c}{a}=\frac{sinC}{sinA}\Rightarrow c=a\frac{sinC}{sinA}\]Ответ: $\angle A={180}^0-\angle B-\angle C$,
\[b=a\frac{sinB}{sinA}, \] \[c=a\frac{sinC}{sinA}.\]Пусть нам даны три стороны треугольника $a,\ b,\ c$. Найдем все углы треугольника.
Решение.
Найдем сначала один из углов по теореме косинусов:
\[c^2=a^2+b^2-2abcosC\] \[2abcosC=a^2+b^2-c^2\] \[\ cosC=\frac{a^2+b^2-c^2}{2ab}\] \[\angle C=arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)\]Используя вновь теорему косинусов, имеем:
\[a^2=c^2+b^2-2cbcosA\] \[2cbcosA=c^2+b^2-a^2\] \[cosA=\frac{c^2+b^2-a^2}{2bc}\] \[\angle A=arc\ cos\left(\frac{c^2+b^2-a^2}{2bc}\right)\]По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C={180}^0\] \[\angle B={180}^0-\angle A-\angle C\]Ответ: $\angle C=arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)$,
\[\angle A=arc\ cos\left(\frac{c^2+b^2-a^2}{2bc}\right),\angle B={180}^0-\angle A-\angle C.\]Пусть нам даны два угла треугольника $A,\ B$ и сторона $b$. Найдем стороны этого треугольника $a,\ c$ и угол $C$.
Решение.
По теореме синусов, имеем
\[\frac{a}{sinA}=\frac{b}{sinB}\] \[a=\frac{bsinA}{sinB}\]По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C={180}^0\] \[\angle C={180}^0-\angle B-\angle A\]По теореме косинусов, имеем:
\[c^2=a^2+b^2-2abcosC\] \[c=\sqrt{a^2+b^2-2abcosC}\]Ответ: $c=\sqrt{a^2+b^2-2abcosC}$,
\[\angle C={180}^0-\angle B-\angle A,\] \[a=\frac{bsinA}{sinB}.\]
















