Правильные многоугольники

Понятие правильного многоугольника

Как мы знаем, сумма углов многоугольника находится по формуле$(n-2)\cdot {180}^0$

Значит, градусная мера одного угла правильного многоугольника равняется

Теорема об описанной около правильного многоугольника окружности

Доказательство.

Существование. Пусть нам дан правильный многоугольник $A_1A_2A_3\dots A_n$. Пусть биссектрисы углов $A_1\ и\ A_2$ пересекаются в точке $O$. Соединим с этой точкой все остальные вершины правильного многоугольника (Рис. 2).

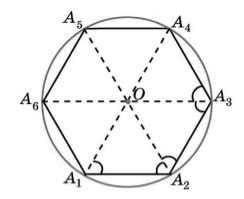
Рисунок 2. Описанная вокруг правильного многоугольника окружность

Так как углы $A_1\ и\ A_2$ равны и $A_1O\ и\ A_2O$ -- биссектрисы, то угол $OA_1A_2$ равен углу $O{A_2A}_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.

Так как $A_1A_2=A_2A_3$, $\angle O{A_2A}_1=\angle O{A_2A}_3$ и сторона $A_2O$ - общая, то треугольники $O{A_2A}_1$ и $O{A_2A}_3$ равны. Следовательно, $OA_2=OA_3$.

Аналогично доказывают другие равенства. В результате, будем иметь

То есть точка $O$ равноудалена от всех вершин многоугольника, а, значит, точка $O$ - центр описанной вокруг правильного многоугольника окружности.

Единственность. Рассмотрим три вершины многоугольника. Очевидно, что через них проходит только одна окружность, следовательно, вокруг правильного многоугольника можно описать только одну окружность.

Теорема доказана.

Теорема вписанной в правильный многоугольник окружности

Доказательство.

Пусть нам дан правильный многоугольник $A_1A_2A_3\dots A_n$. Пусть точка $O$ - центр описанной вокруг данного многоугольника окружности (Рис. 3).

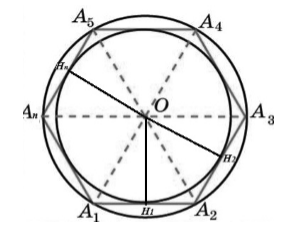
Рисунок 3. Вписанная в правильный многоугольник окружность

Так как углы $A_1\ и\ A_2$ равны и $A_1O\ и\ A_2O$ -- биссектрисы, то угол $OA_1A_2$ равен углу $O{A_2A}_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.

Так как $A_1A_2=A_2A_3$, $\angle O{A_2A}_1=\angle O{A_2A}_3$ и сторона $A_2O$ - общая, то треугольники $O{A_2A}_1$ и $O{A_2A}_3$ равны.

Аналогично доказывается равенство других треугольников. То есть, мы получим

Значит и высоты этих треугольников равны между собой

Тогда окружность с центром в точке $O$ и радиусом, равным ${OH}_1$ проходит через точки $H_1,\ H_2,\dots ,H_n$, то есть касается всех сторон данного многоугольника. Следовательно. Является вписанной для правильного многоугольника.

Единственность. Предположим противное. Пусть существует еще одна вписанная в этот многоугольник окружность. Обозначим её центр $O'$. Тогда $O'$ равноудалена от всех сторон многоугольника, а значит лежит в точке пересечения биссектрис его углов. Но тогда точка $O'$ совпадает с точкой $O$ и, следовательно, эти окружности также совпадают.

Теорема доказана.

Из этих двух теорем можно сформулировать следующие следствия:

Следствие 1: Вписанная в правильный многоугольник окружность касается его в серединах его сторон.

Следствие 2: Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.

Формулы для правильного многоугольника

Дадим теперь несколько формул, относящихся к понятию правильного многоугольника (без их вывода).

Введем следующие обозначения. Пусть $S$ -- площадь правильного многоугольника, $P$ -- периметр правильного многоугольника, $a$ - сторона правильного многоугольника, $r$ - радиус вписанной в правильный многоугольник окружности, $R$ - радиус описанной около правильного многоугольника окружности. Тогда

Пример задачи на понятие правильного многоугольника