Параллельный перенос
Введем определение параллельного переноса на вектор. Пусть нам дан вектор $\overrightarrow{a}$.
Параллельный перенос на вектор $\overrightarrow{a}$ - отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что $\overrightarrow{{MM}_1}=\overrightarrow{a}$ (Рис. 1).
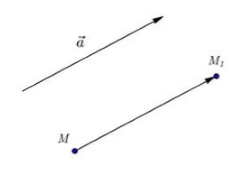
Рисунок 1. Параллельный перенос
Введем следующую теорему.
Параллельный перенос является движением.
Доказательство.
Пусть нам даны точки $M\ и\ N$. Пусть при их параллельном переносе на вектор $\overrightarrow{a}$ эти точки отображаются в точки $M_1$ и $N_1$, соответственно (рис. 2).
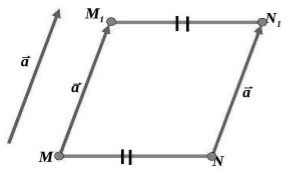
Рисунок 2. Иллюстрация теоремы 1
Так как, по определению 1, $\overrightarrow{{MM}_1}=\overrightarrow{a}$ и $\overrightarrow{{NN}_1}=\overrightarrow{a}$, то , $\overrightarrow{{MM}_1}=\overrightarrow{{NN}_1}$, следовательно, из определения равных векторов получим
Значит четырехугольник ${MM}_1N_1N$ -- параллелограмм и, следовательно, $MN=M_1N_1$. То есть параллельный перенос сохраняет расстояние между точками. Следовательно, параллельный перенос является движением.
Теорема доказана.
Поворот
Введем определение поворота вокруг точки $O$ на угол $\alpha $.
Поворот вокруг точки $O$ на угол $\alpha $ - отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что ${OM}_1=OM,\ \angle M{OM}_1=\angle \alpha $ (Рис. 3).
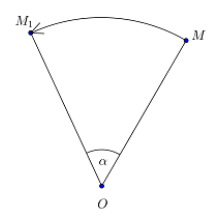
Рисунок 3. Поворот
Введем следующую теорему.
Поворот является движением.
Доказательство.
Пусть нам даны точки $M\ и\ N$. Пусть при их повороте вокруг точки $O$ на угол $\alpha $ они отображаются в точки $M_1$ и $N_1$, соответственно (рис. 4).
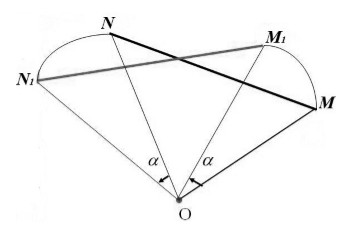
Рисунок 4. Иллюстрация теоремы 2
Так как, по определению 2, ${OM}_1=OM,\ {ON}_1=ON$ и $\overrightarrow{{NN}_1}=\overrightarrow{a}$, а ,$\angle MON=\angle M_1ON_1$, то
Следовательно, $MN=M_1N_1$. То есть поворот сохраняет расстояние между точками. Следовательно, поворот является движением.
Теорема доказана.
Примеры задач на параллельный перенос и поворот
Построить треугольник $A_1B_1C_1$,образованный поворотом вокруг точки $B$ на угол ${45}^0$ равнобедренного прямоугольного (с прямым углом $B)$ треугольника $ABC$.
Решение.
Очевидно, что точка $B$ перейдет сама в себя, то есть $B_1=B$. Так как поворот производится на угол, равный ${45}^0$, а треугольник $ABC$ равнобедренный, то прямая $BA_1$ проходит через точку $L$ -- середины стороны $AC$. По определению, отрезок $BA_1=BA$. Построим его (Рис. 5).
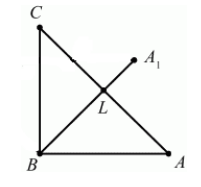
Рисунок 5.
Построим теперь вершину $C_1$ по определению 2:
\[\angle CBC_1={45}^0,\ \ BC=BC_1\]Соединим все вершины треугольника $A_1B_1C_1$ (Рис. 6).
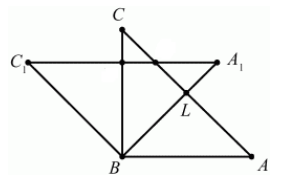
Рисунок 6.
Решение закончено.
Построить параллельный перенос треугольника $ABC$ на вектор $\overrightarrow{BC}$.
Решение.
Перенесем каждую вершину треугольника на вектор $\overrightarrow{BC}$. Получаем треугольник $CA_1C_1$ (рис. 7).
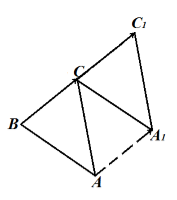
Рисунок 7.
Решение закончено.











