Линейные уравнения с двумя переменными
Уравнение вида $ax+by=c$, где $x\ и\ y$ - неизвестные переменные, а $a,\ b\ и\ c$ - некоторые числа, причем $a\ и\ b$ отличны от нуля, называется линейным уравнением с двумя переменными.
$4x+2y=4$ - линейное уравнение с двумя переменными.
Пара чисел называется решением линейного уравнения с двумя переменными, если при их подстановке в уравнение получается верное равенство.
Пара чисел $(1,\ \ 2)$ является решением линейного уравнения $2x+y=4$.
Свойства линейных уравнений с двумя переменными:
-
К уравнению можно прибавлять с обоих сторон и вычитать из обоих сторон одно и тоже число.
-
Уравнение можно умножать и делить с обоих сторон на одно и тоже, отличное от нуля, число.
Уравнения
\[2x+y=4\] \[2x+y+1=5\] \[3(2x+y+1)=15\]являются равносильными.
График линейного уравнения с двумя переменными
Графиком линейного уравнения с двумя переменными является множество всех точек, которые является решением данного линейного уравнения.
Построим график линейного уравнения $2x-y=-3$
Для этого сначала выразим переменную $y$ через $x$:
\[y=2x+3\]Видим, что мы получили уравнение линейной функции.
Найдем две точки, принадлежащие данной функции. Пусть $x=1$, тогда $y=5$. Пусть $x=-1$, тогда $y=1$. Проведем прямую через точки $\left(-1,1\right)\ и\ (1,\ 5)$. Получим
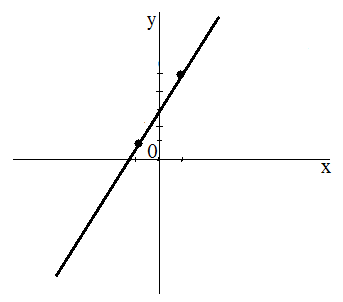
Рисунок 1.
Системы линейных уравнений с двумя переменными
Системой линейных уравнений с двумя переменными называется такая система уравнений, которая в своем составе имеет два и более линейных уравнений с двумя переменными.
Решением системы линейных уравнений называется такая пара чисел, которая является решением всех уравнений, входящих в данную систему.
В дальнейшем будем рассматривать системы из двух линейных уравнений с двумя переменными.
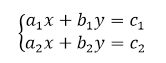
Рисунок 2.
Как мы уже знаем, график каждого из данных уравнений является линейной функцией, а решение любой системы уравнений - пересечение графиков функции каждого из уравнений. Поэтому система двух линейных уравнений с двумя переменными может иметь либо одно решение (в случае, когда прямые пересекутся (рис. 3)) и не иметь решений совсем (если прямые параллельны друг другу(рис. 4))
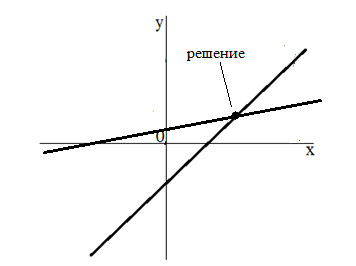
Рисунок 3. Система имеет 1 решение
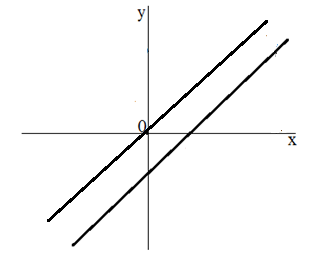
Рисунок 4. Система решений не имеет
Пример решения задачи с использованием понятия линейных уравнений с двумя переменными
Найти графическое решение уравнения $x-y=1$
Решение:
Вначале выразим переменную $y$ через $x$:
\[y=x-1\]Видим, что мы получили уравнение линейной функции.
Найдем две точки, принадлежащие данной функции. Пусть $x=1$, тогда $y=0$. Пусть $x=0$, тогда $y=-1$. Проведем прямую через точки $\left(1,0\right)\ и\ (0,\ -1)$. Получим
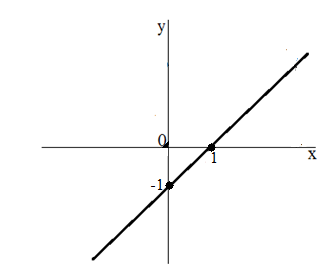
Рисунок 5.
Это и есть графический вид решения системы с двумя переменными.











