Понятие системы линейных уравнений
Для того чтобы раскрыть данное понятие, рассмотрим следующую задачу.
Пусть имеется два числа. Если из первого числа вычесть удвоенное второе число, получим число $6$. Если же к утроенному первому числу прибавить удвоенное второе, то получим число $-6$. Найти эти два числа.
Для решения этой задачи обозначим первое число через $x$, а второе число через $y$.
Так как если из первого числа вычесть удвоенное второе число получим число $6$, то получим следующее уравнение:
\[x-2y=6\]А так как если к утроенному первому числу прибавить удвоенное второе, то получим число $-6$, то имеем уравнение:
\[3x+2y=-6\]Мы получили два разных линейных уравнений с двумя неизвестными. В этом случае для решения данной задачи мы имеем дело с решением системы двух линейных уравнений с двумя переменными.
Системы уравнений записываются следующим образом:
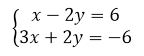
Рисунок 1.
Решением системы линейных уравнений называется такая пара чисел, которая является решением всех уравнений, входящих в данную систему.
Способы решения систем линейных уравнений
Существуют три способа решения систем линейных уравнений:
-
Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
-
Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».
-
Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
Графиком линейного уравнения с двумя переменными является множество всех точек, которые является решением данного линейного уравнения.
Количество корней линейного уравнения
График каждого из уравнений является линейной функцией, а решение любой системы уравнений - пересечение графиков функции каждого из уравнений. Поэтому система двух линейных уравнений с двумя переменными может иметь либо одно решение (в случае, когда прямые пересекутся (рис. 2)) и не иметь решений совсем (если прямые параллельны друг другу(рис. 3))
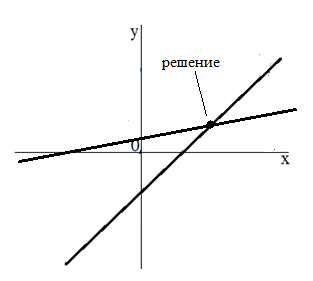
Рисунок 2. Система имеет 1 решение
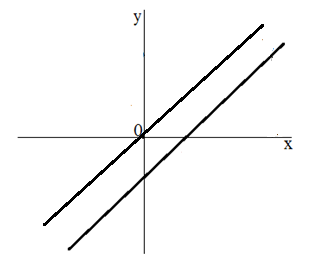
Рисунок 3. Система решений не имеет
В этой главе мы ограничимся нахождением решений систем уравнений графическим способом.
Пример решения задач на использование систем линейных уравнений
Дорешаем задачу 1.
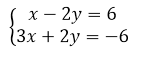
Рисунок 4.
Вначале выразим переменные $y$ через $x$:
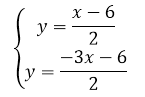
Рисунок 5.
Изобразим решение:
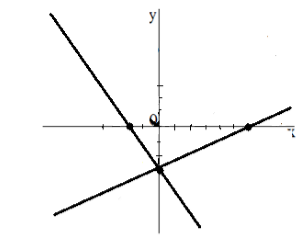
Рисунок 6.
Ответ: $0$ и $-3$.
Составить систему уравнений для данной задачи: Пусть даны два числа. Если второе число умножить на два, то оно будет на $1$ больше первого. Сумма чисел равна $45$. Найти данные числа.
Решение:
Для решения этой задачи обозначим первое число через $x$, а второе число через $y$.
Так как сумма чисел равна $45$, то первое уравнение имеет вид $x+y=45$.
Так как если второе число умножить на два, то оно будет на $1$ больше первого, то второе уравнение имеет вид $2y-x=1$.
Получаем систему:
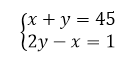
Рисунок 7.













