Определение и основные значения производных
Если существует конечный предел отношения приращения функции $f(x)$ в точке $x_0$ к приращению аргумента $\triangle x$, при $\triangle x\to 0$, то он называется производной функции $f(x)$ в точке $x_0$.
\[{\mathop{lim}_{\triangle x\to 0} \frac{f\left(x_0+\triangle x\right)-f\left(x_0\right)}{\triangle x}\ }={\mathop{lim}_{\triangle x\to 0} \frac{\triangle y}{\triangle x}\ }\]Для вычисления производных пользуются таблицей основных производных (таблица 1)

Рисунок 1. Таблица производных
Правила для вычисления производных
Введем теперь правила для вычисления различных производных.

Рисунок 2.
Производная параметрически заданной функции
Пусть функция задана параметрически
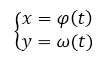
Рисунок 3.
Тогда производная данной функции будет находиться по формуле:
Производная функции, заданной в неявном виде
1 способ: Считают, что в уравнении $F\left(x,y\right)=0$ вместо $y$ подставлена неявная функция $f(x)$, тогда получаем тождество $F\left(x,y\right)=0$, где $y$ - функция от переменной $x$.Дифференцируем это тождество и получаем уравнение $Ф\left(x,y,y'\right)=0$ Выражаем оттуда $y'=U(x,y)$.
2 способ: Вычисление по формуле:
Механический смысл производной
Механический смысл производной состоит в следующем: Скорость материальной очки в момент времени $t$ есть производная пути по времени в этот момент.
Также можно отметить, что ускорение материальной точки в момент времени $t$ есть производная скорости по времени в данный момент времени.
Геометрический смысл производной
Геометрический смысл производной представляет собой угловой коэффициент касательной функции $f(x)$ в точке $x_0$. Иначе также - это тангенс угла наклона касательной к графику данной функции.
Найти производные функции:
а) $f\left(x\right)=x^4$
б) $f\left(x\right)=2-x^3$
в) $f\left(x\right)=3x^7$
г) $f\left(x\right)=x-23$
Решение:
Найдем данные производные с помощью таблицы 1 (рис.1) и правил дифференцирования:
а) $f'\left(x\right)=4x^3$
б) $f'\left(x\right)=-3x^2$
в) $f'\left(x\right)=21x^6$
г) $f'\left(x\right)=1$
Найти производную параметрически заданной функции:
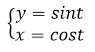
Рисунок 4.
Решение:
\[y'=\frac{(sint)'}{(cost)'}=-\frac{cost}{sint}=-ctgt\]Найти производную степенно-показательной функции
\[f\left(x\right)=x^{cosx}\]Решение:
\[f'\left(x\right)={-sinx\cdot x}^{cosx}\cdot lnx+cosx\cdot x^{cosx-1}\]Найти производную заданной неявно функции:
\[x^2y^2-5x+2y^2+siny=3x-1\]Решение:
Решим первым способом нахождения производных функций, заданных в неявном виде.
\[2yy'x^2-5+4yy'+y'cosy=3\] \[y'(2yx^2+4y+cosy)=8\] \[y'=\frac{8}{2yx^2+4y+cosy}\]











