Пусть y = f(x) -- функция, непрерывная в некотором промежутке a ≤ x ≤ b, причем ее значения принадлежат промежутку c ≤ y ≤ d. Пусть z = F(y) -- функция, непрерывная в промежутке c ≤ y ≤ d. Если принять вышеуказанную функцию как y от х, получаем сложную функцию вида:
Принято говорить, что функция зависит от х через y. Сложная функция будет непрерывной в промежутке a ≤ x ≤ b, поскольку бесконечно малому приращению x соответствует бесконечно малое приращение z в силу непрерывности f(y).
Если функция z имеет производную при $y = y_0$, то справедливо следующее выражение:
$\Delta z=F(y_{0} +\Delta y)-F(y_{0} )=\left[F`(y_{0} )+\alpha \right]\Delta y$ (1)
где $\alpha $ -- функция $\Delta $y, определенная при всех $\Delta $y близких и отличных от нуля.
Причем $\alpha $ $\to $0, если $\Delta $y $\to $0, даже принимая равное нулю значение.
Если y=f(x) имеет в точке x=x0 производную f`(x0) и z=F(y) имеет в точке y0=f(x0) производную F`(y0), то сложная функция F(f(x)) имеет в точке x=x0 производную, равную произведению F`(y0) f `(x0).
Пусть $\Delta $х -- приращение, которое придается х0 независимой переменной х, и $\Delta $y = f(x0+ $\Delta $х) -- f(x0) -- соответствующее приращение переменной y.
Пусть $\Delta $z = F(y0+ $\Delta $y) -- F(y0). Производная от сложной функции z = F(f(x)) по x при x=x0 равна пределу отношения $\Delta $z/$\Delta $х при $\Delta $х $\to $0, если этот предел существует. Разделим выражение (1) на $\Delta $х:
\[\frac{\Delta z}{\Delta x} =\left[F`(y_{0} )+\alpha \right]\frac{\Delta y}{\Delta x} \]При стремлении $\Delta $х к нулю и $\Delta $y $\to $0, в силу непрерывности функции y=f(x) в точке x=x0, а потому $\alpha $$\to $0. Отношение $\Delta $y/$\Delta $х стремится при этом к производной f `(x0):
\[\mathop{\lim }\limits_{\Delta x\to 0} \frac{\Delta z}{\Delta x} =F`(y_{0} )f`(x_{0} )\]Что доказывает теорему.
Производная сложной функции равна произведению производной по промежуточной переменной по независимой переменной:
\[Z'x=F`\left(y\right)f'\left(x\right)\]Формула нахождения производной сложной функции на примере:
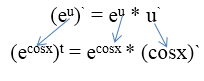
Найти производную сложной функции
\[y=\sqrt{5x^{2} +2x-1} \]Решение.
По правилу нахождения производной сложной функции вычислим производную и умножим ее на производную подкоренного выражения.
\[y'=\left(\sqrt{3x^{2} +x-1} \right)^{{'} } =\frac{1}{2\sqrt{3x^{2} +x-1} } \left(3x^{2} +x-1\right)^{{'} } =\] \[=\frac{3\cdot 2x+1}{2\sqrt{3x^{2} +x-1} } =\frac{6x+1}{2\sqrt{3x^{2} +x-1} } \]Найти производную сложной функции
\[y=e^{3x+2} \]Решение.
По правилу нахождения производной сложной функции вычислим производную экспоненты и умножим ее на производную степени.
\[y'=\left(e^{3x+2} \right)^{{'} } =e^{3x+2} \cdot (3x+2)'=e^{3x+2} \cdot 3=3e^{3x+2} \]Найти производную сложной функции
\[y=9\cdot arctg^{12} (4\cdot \ln x)\]Решение.
- Вынесем константу за знак производной \[y'=9\left(arctg^{12} (4\cdot \ln x)\right)^{{'} } \]
- По правилу нахождения производной сложной функции найдем производную от степени arctg. \[y'=9\left(arctg^{12} (4\cdot \ln x)\right)^{{'} } =9\cdot 12\cdot (arctg(4\cdot \ln x))^{11} \cdot (arctg(4\cdot \ln x))'=\]
- Теперь найдем производную тригонометрической функции внутри скобки. \[(arctg(4\cdot \ln x))'=\frac{1}{1+(4\cdot \ln x)^{2} } (4\cdot \ln x)'=\frac{1}{1+16\cdot \ln x^{2} } (4\cdot \ln x)'\] \[y'=108\cdot (arctg(4\cdot \ln x))^{11} \cdot \frac{1}{1+16\cdot \ln x^{2} } (4\cdot \ln x)'=108\cdot (arctg(4\cdot \ln x))^{11} \cdot \frac{1}{1+16\cdot \ln x^{2} } \frac{4}{x} =432\frac{arctg^{11} (4\cdot \ln x)}{x\cdot (1+16\cdot \ln ^{2} x)} (4\cdot \ln x)\]
Найти производную сложной функции
\[y=\arcsin 2^{x} \]Решение.
\[y'=\left(\arcsin 2^{x} \right)^{{'} } =\frac{1}{\sqrt{1-(2^{x} )^{2} } } (2^{x} )'=\frac{1}{\sqrt{1-2^{2x} } } 2^{x} \ln 2=\frac{2^{x} \ln 2}{\sqrt{1-2^{2x} } } \]Найти производную сложной функции
\[y=7\cdot \ln \cdot \sin^{3} x\]Решение.
\[y'=\left(7\cdot \ln \cdot \sin {}^{3} x\right)^{{'} } =7\cdot \left(\ln \cdot \sin {}^{3} x\right)^{{'} } =7\cdot \frac{1}{\sin {}^{3} x} \left(\sin {}^{3} x\right)^{{'} } =\] \[7\cdot \frac{1}{\sin {}^{3} x} \cdot 3\cdot \sin {}^{2} x\left(\sin x\right)^{{'} } =21\cdot \frac{1}{\sin x} \cdot \frac{\cos x}{\sin x} =21\cdot ctgx\]












