Левой производной функции f(x) в точке х называется левый предел отношения приращения функции $\Delta $y к приращению аргумента $\Delta $х, когда $\Delta $х$\to $0:
\[f'_{-} (x)=\mathop{\lim }\limits_{\Delta x\to 0-0} \frac{\Delta y}{\Delta x} \]Правой производной функции f(x) в точке х называется правый предел отношения приращения функции $\Delta $y к приращению аргумента $\Delta $х, когда $\Delta $х$\to $0:
\[f'_{+} (x)=\mathop{\lim }\limits_{\Delta x\to 0+0} \frac{\Delta y}{\Delta x} \]Для того, чтобы функция f(x) имела производную в точке х, необходимо и достаточно, чтобы в этой точке функция была непрерывна, и существовали односторонние производные f`-(x) и f`+(x), равные между собой.
Если \[f'_{-} (x)\ne f'_{+} (x)\]то в точке x производной не существует, и график функции имеет излом (рис. 1).
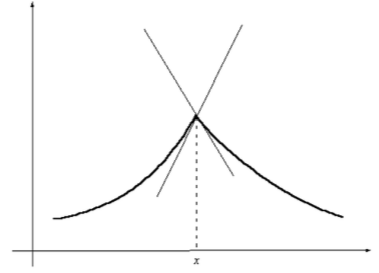
Рисунок 1. Излом функции
Найти левую и правую производные в точке $x_0 = 0$ функции:
y = $| \Delta x|$Решение.
\[f'_{-} (0)=\mathop{\lim }\limits_{\Delta x\to 0-} \frac{\Delta y}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0-} \frac{f(0+\Delta x)-f(0)}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0-} \frac{\left|\Delta x\right|-0}{\Delta x} =\frac{\left|\Delta x\right|}{\Delta x} \]Так как $\Delta $х$\to $0-, то $\Delta $х является маленькой отрицательной величиной, а тогда по определению модуля $|\Delta х|$ = -$\Delta $х. Отсюда
\[f'_{-} (0)=\mathop{\lim }\limits_{\Delta x\to 0-} \frac{\left|\Delta x\right|}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0-} \frac{-\left|\Delta x\right|}{\Delta x} =-1\]Аналогично найдем правую производную
\[f'_{+} (0)=\mathop{\lim }\limits_{\Delta x\to 0+} \frac{\Delta y}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0+} \frac{f(0+\Delta x)-f(0)}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0+} \frac{\left|\Delta x\right|-0}{\Delta x} =\frac{\left|\Delta x\right|}{\Delta x} \] \[f'_{+} (0)=\mathop{\lim }\limits_{\Delta x\to 0+} \frac{\left|\Delta x\right|}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0-} \frac{+\left|\Delta x\right|}{\Delta x} =1\]Графически это означает, что функция имеет излом в точке = 0
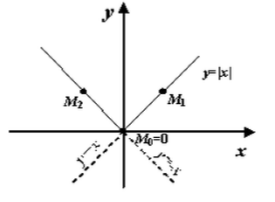
Рисунок 2. Излом функции
\[y=\left|x\right|=\left\{\begin{array}{c} {-x,\begin{array}{cc} при & {xВычислить производные функции:
\[y=\left|x^{2} -1\right|\]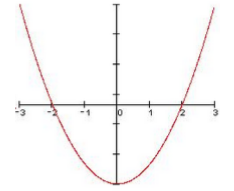
Рисунок 3. График функции
Решение.
Из графика функции видно, что производная не существует в точках -2 и 2. Найдем односторонние производные.
а) Левая производная
\[f'_{-} (0)=\mathop{\lim }\limits_{\Delta x\to 0-} \frac{\left|(2+\Delta x)^{2} -4\right|-\left|2^{2} -4\right|}{\Delta x} =-4\] \[f'_{-} (0)=\mathop{\lim }\limits_{\Delta x\to 0-} \frac{\left|(-2+\Delta x)^{2} -4\right|-\left|\left(-2\right)^{2} -4\right|}{\Delta x} =-4\]б) Правая производная
\[f'_{+} (0)=\mathop{\lim }\limits_{\Delta x\to 0+} \frac{\left|(2+\Delta x)^{2} -4\right|-\left|2^{2} -4\right|}{\Delta x} =4\] \[f'_{+} (0)=\mathop{\lim }\limits_{\Delta x\to 0+} \frac{\left|(2+\Delta x)^{2} -4\right|-\left|2^{2} -4\right|}{\Delta x} =4\]Вывод: Правая производная при 2 и -2 существует и равна 4. Левая производная при 2 и -2 существует и равна -4.
Найдем производные при х=1.
\[\mathop{\lim }\limits_{\Delta x\to 0} \frac{\left|(1+\Delta x)^{2} -4\right|-\left|1^{2} -4\right|}{\Delta x} =-2\] \[\mathop{\lim }\limits_{\Delta x\to 0-} \frac{\left|(1+\Delta x)^{2} -4\right|-\left|1^{2} -4\right|}{\Delta x} =-2\] \[\mathop{\lim }\limits_{\Delta x\to 0+} \frac{\left|(1+\Delta x)^{2} -4\right|-\left|1^{2} -4\right|}{\Delta x} =-2\]Значит, производная в точке 1 существует и равна -2












