Понятие производной можно применять для построения графиков функций, так как с помощью производных мы можем выяснить промежутки возрастания и убывания, промежутки выпуклости и вогнутости функции, найти точки экстремума функции (точки минимума и максимума), а также наибольшее и наименьшее значения функции данной функции. Однако, помимо этих данных, для более точного построения графиков функции нам необходимы еще некоторые сведения. Поэтому вначале приведем схему исследования функций, которой и будем пользоваться в дальнейшем.
Схема для исследования функций
-
Найти область определения функции;
-
Найти область значения функции;
-
Выяснить является ли функция четной, нечетной и периодической.
-
Найти точки пересечения с осями координат;
-
Выяснить промежутки знакопостоянства функции;
-
Найти производную функции;
-
Найти точки минимума и максимума функции;
-
Найти промежутки монотонности функции;
-
Найти наибольшее и наименьшее значение функции;
-
Найти вторую производную функции;
-
Найти промежутки выпуклости и вогнутости функции;
-
Найти пределы функции на концах области определения;
-
Если необходимо, найти значение функции в дополнительных точках;
-
Построить график функции.
Задачи на исследование и построение графиков функций.
Исследовать и построить график функции:
\[y=2x+1\]-
Область определении - все действительные числа.
-
Область значения - все действительные числа.
-
функция ни четна, ни нечетна, непериодическая.
-
Точки пересечения с осями координат:
При $y=0$, $2x+1=0,\ x=-\frac{1}{2}$. Точка пересечения с осью $Ox:\left(-\frac{1}{2},0\right)$.
При $x=0$, $y=1$. Точка пересечения с осью $Ox:\left(0,1\right)$.
-
При $x\in \left(-\infty ,-\frac{1}{2}\right)$ функция отрицательна, при $x\in \left(-\frac{1}{2},\infty \right)$ функция положительна.
-
Производная:
\[y'=2>0\] -
Точек минимума и максимума нет.
-
Функция возрастает на всей области определения.
-
Функция не имеет наибольшего и наименьшего значений.
-
$y''=0$
-
Функция не имеет промежутков выпуклости и вогнутости.
-
${\mathop{lim}_{x\to -\infty } y\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } y\ }=+\infty $
-
График:
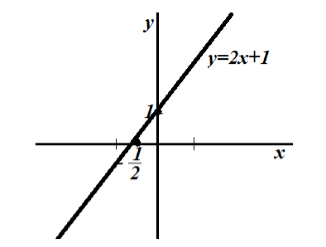
Рисунок 1.
Исследовать и построить график функции:
\[y=\frac{5x^2+x+1}{x}\]-
Область определения: $\left(-\infty ,0\right)(0,\infty )$.
-
Область значения:$\left(-\infty ,1-2\sqrt{5}\right][1+2\sqrt{5},\infty )$
-
Функция ни четна, ни нечетна, непериодическая.
-
Точек пересечения с осями координат нет.При $x\in \left(-\infty ,0\right)$ функция отрицательна, при $x\in \left(0,\infty \right)$ функция положительна.
-
При $x\in \left(-\infty ,0\right)$ функция отрицательна, при $x\in \left(0,\infty \right)$ функция положительна.
-
Производная:
\[y'=\frac{10x^2+x-5x^2-x-1}{x^2}=\frac{5x^2-1}{x^2}\] -
Найдем точки минимума:
\[\frac{5x^2-1}{x^2}=0\] \[x\ne 0,\ x=\pm \frac{\sqrt{5}}{5}\]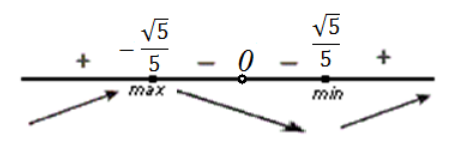
Рисунок 2.Максимум функции: $\left(-\frac{\sqrt{5}}{5},1-2\sqrt{5}\right)$
Минимум функции: $\left(\frac{\sqrt{6}}{6},1+2\sqrt{5}\right)$
-
Из рисунка выше видим, что функция возрастает при $x\in \left(-\infty ,-\frac{\sqrt{5}}{5}\right)\left(\frac{\sqrt{5}}{5},\infty \right)$ и убывает при $x\in \left(-\frac{\sqrt{5}}{5},0\right)\left(0,\frac{\sqrt{5}}{5}\right)$
-
Наибольшее и наименьшее значение:
$f\left(-\frac{\sqrt{5}}{5}\right)=1-2\sqrt{5}$ - наименьшее значение,
$f\left(\frac{\sqrt{5}}{5}\right)=1-2\sqrt{5}$ - наибольшее значение.
-
$y''=\frac{{10x}^3-{10x}^3+2x}{x^4}=\frac{2}{x^3}$
-
Найдем промежутки выпуклости и вогнутости:
\[\frac{2}{x^3}=0\] \[x\ne 0\]Методом интервалов получаем, что
Функция вогнута при $x\in \left(0,\infty \right)$ и выпукла при $x\in \left(-\infty ,0\right)$.
-
${\mathop{lim}_{x\to 0-0} y\ }=-\infty $, ${\mathop{lim}_{x\to 0+0} y\ }=+\infty $, ${\mathop{lim}_{x\to -\infty } y\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } y\ }=+\infty $
-
График:
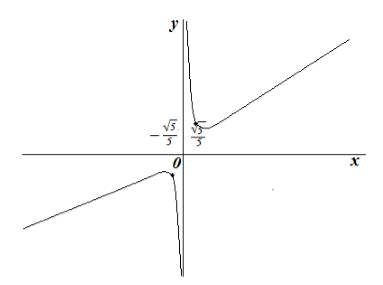
Рисунок 3.












