Что такое бесконечные малые функции
Функции являются бесконечно малыми, если при стремлении x к точке а их предел равен 0.
\[\mathop{\lim }\limits_{x\to a} f(x)=0\]Однако бесконечно малой функция может быть только в конкретной точке. Как показано на рисунке 1, функция бесконечно мала только в точке 0.
Рисунок 1. Бесконечно малая функция
Если предел частного двух функций в результате дает 1, функции называются эквивалентными бесконечно малыми при стремлении х к точке а.
\[\mathop{\lim }\limits_{x\to a} \frac{f(x)}{g(x)} =1\]Если функции f(x), g(x) бесконечно малые при $х > а$, то:
- Функция f(x) называется бесконечно малой высшего порядка относительно g(x), если выполняется условие: \[\mathop{\lim }\limits_{x\to a} \frac{f(x)}{g(x)} =0\]
- Функция f(x) называется бесконечно малой n-го порядка относительно g(x), если отличен от 0 и конечен предел: \[\mathop{\lim }\limits_{x\to a} \frac{f(x)}{g^{n} (x)} =A\]
Функция $y=х^3$ является бесконечно малой высшего порядка при х>0, в сравнении с функцией y=5x, так как предел их отношения равен 0, это объясняется тем, что функция $y=х^3$ стремится к нулевому значению быстрее:
\[\mathop{\lim }\limits_{x\to 0} \frac{x^{2} }{5x} =\frac{1}{5} \mathop{\lim }\limits_{x\to 0} x=0\]Функции y=x2-4 и y=x2-5x+6 являются бесконечно малыми одного порядка при х>2, так как предел их отношения не равен 0:
\[\mathop{\lim }\limits_{x\to 2} \frac{x^{2} -4}{x^{2} -5x+6} =\mathop{\lim }\limits_{x\to 2} \frac{(x-2)(x+2)}{(x-2)(x-3)} =\mathop{\lim }\limits_{x\to 2} \frac{(x+2)}{(x-3)} =\frac{4}{-1} =-4\ne 0\]Свойства эквивалентных бесконечно малых
- Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.
- Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.
Из первого свойства следует, что эквивалентные бесконечно малые могут стать приближенно равными со сколь угодно малой относительной погрешностью. Поэтому знак ≈ применяется как для обозначения эквивалентности бесконечно малых, так и для записи приближенного равенства их достаточно малых значений.
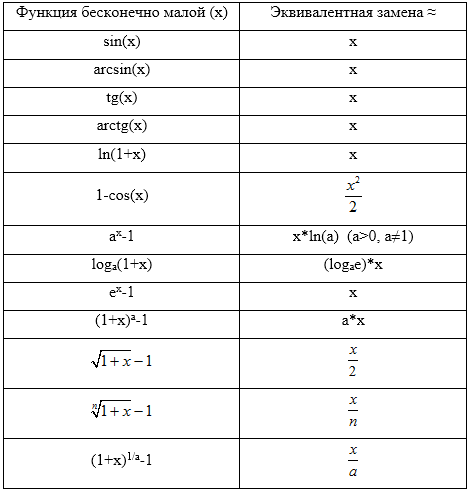
При нахождении пределов очень часто приходится применять замену эквивалентных функций для быстроты и удобства вычислений. Таблица эквивалентных бесконечно малых представлена ниже (табл.1).
Эквивалентность бесконечно малых приведенных в таблице можно доказать, опираясь на равенство:
\[\mathop{\lim }\limits_{x\to a} \frac{f(x)}{g(x)} =1\]Таблица 1
Замена эквивалентных величин
Докажем эквивалентность бесконечно малых ln(1+x) и x.
Доказательство:
- Найдем предел отношения величин \[\mathop{\lim }\limits_{x\to a} \frac{\ln (1+x)}{x} \]
- Для этого применим свойство логарифма: \[\frac{\ln (1+x)}{x} =\frac{1}{x} \ln (1+x)=\ln (1+x)^{\frac{1}{x} } \] \[\mathop{\lim }\limits_{x\to a} \frac{\ln (1+x)}{x} =\mathop{\lim }\limits_{x\to a} \ln (1+x)^{\frac{1}{x} } \]
- Зная, что логарифмическая функция непрерывна в своей области определения, можно поменять местами знак предела и логарифмической функции: \[\mathop{\lim }\limits_{x\to a} \frac{\ln (1+x)}{x} =\mathop{\lim }\limits_{x\to a} \ln (1+x)^{\frac{1}{x} } =\ln \left(\mathop{\lim }\limits_{x\to a} (1+x)^{\frac{1}{x} } \right)\]
- Поскольку х -- бесконечно малая величина, предел стремиться к 0. Значит: \[\mathop{\lim }\limits_{x\to a} \frac{\ln (1+x)}{x} =\mathop{\lim }\limits_{x\to a} \ln (1+x)^{\frac{1}{x} } =\ln \left(\mathop{\lim }\limits_{x\to 0} (1+x)^{\frac{1}{x} } \right)=\ln e=1\]
(применили второй замечательный предел)
Ответ: равенство частного единице доказывает эквивалентность величин.
Найти предел
\[\mathop{\lim }\limits_{x\to 0} \frac{1-\cos (3x)}{2x^{2} } \]Решение:
- Вычислим предел стандартным способом: \[\mathop{\lim }\limits_{x\to 0} \frac{1-\cos (3x)}{2x^{2} } =\frac{1-\cos (3*0)}{2*0^{2} } =\left\langle \frac{0}{0} \right\rangle \]
- В таблице эквивалентности найдем замену числителю величины: \[\mathop{\lim }\limits_{x\to 0} \frac{1-\cos (3x)}{2x^{2} } =\frac{\frac{\left(3x\right)^{2} }{2} }{2x^{2} } =\frac{9x^{2} }{4x^{2} } =\frac{9}{4} =2,25\]
(неопределенность)














