Определение эмпирической функции распределения
Пусть $X$ -- случайная величина. $F(x)$ - функция распределения данной случайной величины. Будем проводить в одних и тех же независимых друг от друга условий $n$ опытов над данной случайной величиной. При этом получим последовательность значений $x_1,\ x_2\ $, ... ,$\ x_n$, которая и называется выборкой.
Каждое значение $x_i$ ($i=1,2\ $, ... ,$ \ n$) называется вариантой.
Функция распределения $F(x)$ генеральной совокупности называется теоретической функцией распределения.
Одной из оценок теоретической функции распределения является эмпирическая функция распределения.
Эмпирической функцией распределения $F_n(x)$ называется функция, которая определяет для каждого значения $x$ относительную частоту события $X \[F_n\left(x\right)=\frac{n_x}{n}\]
где $n_x$ - число вариант, меньших $x$, $n$ -- объем выборки.
Отличие эмпирической функции от теоретической состоит том, что теоретическая функция определяет вероятность события $X
Свойства эмпирической функции распределения
Рассмотрим теперь несколько основных свойств функции распределения.
-
Область значений функции $F_n\left(x\right)$ -- отрезок $[0,1]$.
-
$F_n\left(x\right)$ неубывающая функция.
-
$F_n\left(x\right)$ непрерывная слева функция.
-
$F_n\left(x\right)$ кусочно-постоянная функция и возрастает только в точках значений случайной величины $X$
-
Пусть $X_1$ -- наименьшая, а $X_n$ -- наибольшая варианта. Тогда $F_n\left(x\right)=0$ при ${x\le X}_1$и $F_n\left(x\right)=1$ при $x\ge X_n$.
Введем теорему, которая связывает между собой теоретическую и эмпирическую функции.
Пусть $F_n\left(x\right)$ -- эмпирическая функция распределения, а $F\left(x\right)$ -- теоретическая функция распределения генеральной выборки. Тогда выполняется равенство:
\[{\mathop{lim}_{n\to \infty } {|F}_n\left(x\right)-F\left(x\right)|=0\ }\]Примеры задач на нахождение эмпирической функции распределения
Пусть распределение выборки имеет следующие данные, записанные с помощью таблицы:

Рисунок 1.
Найти объем выборки, составить эмпирическую функцию распределения и построить её график.
Решение:
Объем выборки: $n=5+10+15+20=50$.
По свойству 5, имеем, что при $x\le 1$ $F_n\left(x\right)=0$, а при $x>4$ $F_n\left(x\right)=1$.
Значение $x
Значение $x
Значение $x
Таким образом, получаем:
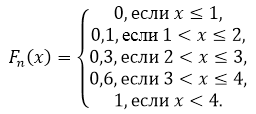
Рисунок 2.
Построим график эмпирического распределения:
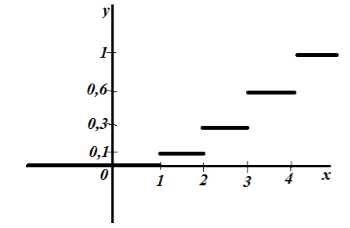
Рисунок 3.
Из городов центральной части России случайным образом выбрано 20 городов, для которых получены следующие данные по стоимости проезда в общественном транспорте: 14, 15, 12, 12, 13, 15, 15, 13, 15, 12, 15, 14, 15, 13, 13, 12, 12, 15, 14, 14.
Составить эмпирическую функцию распределения данной выборки и построить её график.
Решение:
Запишем значения выборки в порядке возрастания и посчитаем частоту каждого значения. Получаем следующую таблицу:

Рисунок 4.
Объем выборки: $n=20$.
По свойству 5, имеем, что при $x\le 12$ $F_n\left(x\right)=0$, а при $x>15$ $F_n\left(x\right)=1$.
Значение $x
Значение $x
Значение $x
Таким образом, получаем:
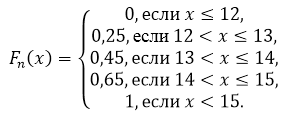
Рисунок 5.
Построим график эмпирического распределения:
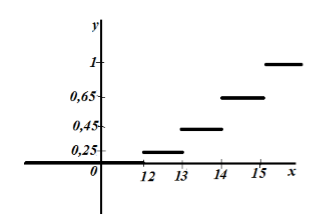
Рисунок 6.
Оригинальность: $92,12\%$.












