Число а является пределом последовательности, если для любого положительного $\varepsilon $ можно подобрать такой номер N члена последовательности, что для всех членов последовательности с номерами n $>$ N будет верно неравенство:
числовая последовательностьЕсли предел последовательности найти невозможно, то говорят что «последовательность расходится».
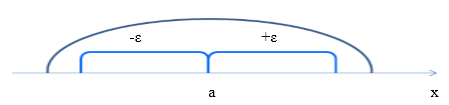
Рисунок 1. Окрестность точки а
Если последовательность $х_n$ имеет предел, то он единственный.
Действительно, если бы числовая последовательность имела два предела a и b, то окрестность точки а (а -- $\varepsilon $$;$ а + $\varepsilon $) и точки b (b -- $\varepsilon $$;$ b + $\varepsilon $) должны были бы содержать все члены последовательности равновозможно. Но интервалы не пересекаются, поэтому это невозможно.
Если последовательность $х_n$ монотонно возрастает (убывает) и ограничена сверху (снизу), то она имеет предел.
Рассмотрим случай неубывающей последовательности. Пусть числовая последовательность \{хn\} ограничена сверху числом b. Тогда для последовательности существует четко определенная верхняя грань M ≤ b. В этом случае для каждого члена последовательности найдется такое $n = n_0$, что M -- $\varepsilon n_0$.
\[M-\varepsilon А значит, предел последовательности существует.Найти предел числовой последовательности
\[1,\frac{1}{2} ,\frac{1}{3} ...\frac{1}{n} \]Решение:
\[\mathop{\lim }\limits_{x\to \infty } \frac{1}{n} =0\]Вывод: Чем больше номер члена последовательности, тем дальше от предельного значения он лежит.
Найти предел числовой последовательности
\[\frac{1}{2} ,\frac{2}{3} ,\frac{3}{4} ...\frac{n}{n+1} \]Решение:
Поскольку
\[\left|\frac{n}{n+1} -1\right|=\frac{1}{n+1} \]То для любого $\varepsilon > 0$ найдется такое натуральное число Nб, при котором будет справедливо неравенство:
\[\frac{1}{n+1} Поэтому мы вправе взять любое N удовлетворяющее неравенству. Например - 1. \[\mathop{\lim }\limits_{x\to \infty } \frac{n}{n+1} =1\]Вывод: Последовательность сходится, и чем больше номер члена последовательности, тем дальше от предельного числа он лежит.
Определить сходимость последовательности и найти ее предел
$2, 0, 3, 0, 3, 2, 0 \dots$
Очевидно, что последовательность не сходится, а значит, и не имеет предела.
Утверждения о пределе последовательности:
- К нулю всегда сходятся последовательности вида: \[\mathop{\lim }\limits_{x\to \infty } \frac{1}{n} =0\] \[\mathop{\lim }\limits_{x\to \infty } a^{n} =0\begin{array}{cc} {} & {\left|a\right|} \end{array}Предел постоянной последовательности всегда равен ее постоянному члену. \[\mathop{\lim }\limits_{x\to \infty } a=a\]
Если $\mathop{\lim }\limits_{x\to \infty } a_{n} =a$, а $\mathop{\lim }\limits_{x\to \infty } b_{n} =b$, то:
- $\mathop{\lim }\limits_{x\to \infty } (a_{n} \pm b_{n} )=a\pm b$
- $\mathop{\lim }\limits_{x\to \infty } (a_{n} \cdot b_{n} )=a\cdot b$
- $\mathop{\lim }\limits_{x\to \infty } (a_{n} /b_{n} )=a/b\begin{array}{cc} {} & {b\ne 0} \end{array}$
Вычислить
\[\mathop{\lim }\limits_{x\to \infty } \frac{1}{n^{2} } \]Решение:
$\frac{1}{n^{2} } =\frac{1}{n} \cdot \frac{1}{n} $ и $\frac{1}{n} \to 0$, то
\[\frac{1}{n^{2} } \to 0\cdot 0=0\]А значит,
\[\mathop{\lim }\limits_{x\to \infty } \frac{1}{n^{2} } =0\]Вывод, любая последовательность вида $\frac{1}{n^{k} } \to 0$
Вычислить
\[\mathop{\lim }\limits_{x\to \infty } \frac{\frac{3n^{2} }{n^{2} } -\frac{2n}{n^{2} } +\frac{2}{n^{2} } }{\frac{n^{2} }{2n^{2} } -\frac{n}{n^{2} } +\frac{1}{n^{2} } } =\mathop{\lim }\limits_{x\to \infty } \frac{3-2\cdot \frac{1}{n} +2\cdot \frac{1}{n^{2} } }{\frac{1}{2} -\frac{1}{n} +\frac{1}{n^{2} } } \]Используя полученные ранее выводы $\frac{1}{n} \to 0$
\[\mathop{\lim }\limits_{x\to \infty } \frac{3-2\cdot \frac{1}{n} +2\cdot \frac{1}{n^{2} } }{\frac{1}{2} -\frac{1}{n} +\frac{1}{n^{2} } } =\frac{3-2\cdot 0+2\cdot 0}{\frac{1}{2} -0+0} =6\]











