Если функция f(x) имеет предел b при х>$\infty $, ее можно представить в виде суммы числа b и бесконечно малой функции.
Пусть
\[\mathop{\lim }\limits_{x\to \infty } f(x)=b\]Тогда разность
\[f(x)-b=\alpha (x)\]Докажем, что $\alpha $(х) бесконечно малая функция при х > $\infty $.
\[\left|f(x)-b\right|Это значит, что |$\alpha $(х)| $$ N, т.е. $\alpha $(х) - бесконечно малая функция и \[f(x)=b+\alpha (x)\]Из доказательства теоремы 1:
\[f(x)=b+\alpha (x),\]где $\alpha $(х) бесконечно малая функция при х>$\infty $.
Докажем, что
\[\mathop{\lim }\limits_{x\to \infty } f(x)=b\]Поскольку $f(x)-b=\alpha (x)$, и |$\alpha $(х)| $$ N, имеем:
\[\left|f(x)-b\right|И значит \[\mathop{\lim }\limits_{x\to \infty } f(x)=b\]Доказать равенство
\[\mathop{\lim }\limits_{x\to \infty } \left(3+\frac{1}{x} -\frac{1}{x^{2} } \right)=3\]Доказательство: Поскольку в равенстве мы наблюдаем две бесконечно малые функции, их разность также бесконечно малая величина х>$\infty $. А значит, по теореме 2 предел суммы числа А и бесконечно малой функции равен числу А.
\[\mathop{\lim }\limits_{x\to \infty } \left(3+\frac{1}{x} -\frac{1}{x^{2} } \right)=3\]Если $\mathop{\lim }\limits_{x\to \infty } f(x)=b$ и $\mathop{\lim }\limits_{x\to \infty } g(x)=c$, то функции f(x)+g(x) или f(x)-g(x) также имеют пределы при х>$\infty $:
\[\mathop{\lim }\limits_{x\to \infty } \left[f(x)\pm g(x)\right]=\mathop{\lim }\limits_{x\to \infty } f(x)\pm \mathop{\lim }\limits_{x\to \infty } g(x)\]т.е. предел суммы или разности двух функций равен сумме (разности) их пределов.
Данная теорема применяется для суммы любого конечного числа функций!
По теореме 1 функции можно представлять в виде:
$f(x)=b+\alpha (x)$ и $g(x)=c+\beta (x)$Тогда,
\[f(x)+g(x)=b+\alpha (x)+c+\beta (x)=(b+c)+(\alpha (x)+\beta (x))\]Сумма $\alpha $(х)+$\beta $(х) является бесконечно малой функцией. А значит, равенство состоит из суммы чисел и бесконечно малой величины, поэтому можно применить теорему 2.
\[\mathop{\lim }\limits_{x\to \infty } \left[f(x)+g(x)\right]=b+c=\mathop{\lim }\limits_{x\to \infty } f(x)+\mathop{\lim }\limits_{x\to \infty } g(x)\]Аналогично доказывается разность функций.
Если $\mathop{\lim }\limits_{x\to \infty } f(x)=b$ и $\mathop{\lim }\limits_{x\to \infty } g(x)=c$, то функция f(x)*g(x) имеет предел при х>$\infty $:
\[\mathop{\lim }\limits_{x\to \infty } \left[f(x)g(x)\right]=\mathop{\lim }\limits_{x\to \infty } f(x)\cdot \mathop{\lim }\limits_{x\to \infty } g(x)\]По теореме 1 функции можно представлять в виде:
$f(x)=b+\alpha (x)$ и $g(x)=c+\beta (x)$Тогда,
\[f(x)g(x)=\left[b+\alpha (x)\right]\cdot \left[c+\beta (x)\right]=bc+\left[c\alpha (x)+b\beta (x)+\alpha (x)\beta (x)\right]\]Сумма с$\alpha $(х)+b$\beta $(х)+$\alpha $(х)$\beta $(х) является бесконечно малой функцией. А значит, равенство состоит из суммы чисел и бесконечно малой величины, поэтому можно применить теорему 2.
\[\mathop{\lim }\limits_{x\to \infty } \left[f(x)g(x)\right]=\mathop{\lim }\limits_{x\to \infty } f(x)\cdot \mathop{\lim }\limits_{x\to \infty } g(x)\]Следствием данной теоремы является свойство о возможности вынести постоянный множитель за знак предела:
\[\mathop{\lim }\limits_{x\to a} C*f(x)=C\mathop{*\lim }\limits_{x\to a} f(x)\]Данная теорема применима к любому конечному числу равных сомножителей.
Если $\mathop{\lim }\limits_{x\to \infty } f(x)=b$ , $\mathop{\lim }\limits_{x\to \infty } g(x)=c$, причем с ≠0, то функция f(x)/g(x) имеет предел при х>$\infty $:
\[\mathop{\lim }\limits_{x\to \infty } \left[\frac{f(x)}{g(x)} \right]=\frac{\mathop{\lim }\limits_{x\to \infty } f(x)}{\mathop{\lim }\limits_{x\to \infty } g(x)} \]По теореме 1 функции можно представлять в виде:
$f(x)=b+\alpha (x)$ и $g(x)=c+\beta (x)$
Рассмотрим разность,
\[\frac{f(x)}{g(x)} -\frac{b}{c} =\frac{b+\alpha (x)}{c+\beta (x)} -\frac{b}{c} =\frac{c\alpha (x)-b\beta (x)}{c^{2} +c\beta (x)} \]Дробь
\[\frac{c\alpha (x)-b\beta (x)}{c^{2} +c\beta (x)} =\gamma (x)\]Является бесконечно малой функцией, поскольку числитель (разность бесконечно малых) есть бесконечно малая величина, а знаменатель удовлетворяет требованию $c ≠0$. Значит:
\[\frac{f(x)}{g(x)} =\frac{b}{c} +\frac{c\alpha (x)-b\beta (x)}{c^{2} +c\beta (x)} =\frac{b}{c} +\gamma (x)\]По теореме 2, разность функций имеют предел, равный отношению b/c.
\[\mathop{\lim }\limits_{x\to \infty } \left[\frac{f(x)}{g(x)} \right]=\frac{b}{c} =\frac{\mathop{\lim }\limits_{x\to \infty } f(x)}{\mathop{\lim }\limits_{x\to \infty } g(x)} \]Найти предел функции:
\[\mathop{\lim }\limits_{x\to 2} (x^{2} +3x-4)\]Решение:
\[\mathop{\lim }\limits_{x\to 2} (x^{2} +3x-4)=\mathop{\lim }\limits_{x\to 2} x^{2} +\mathop{\lim }\limits_{x\to 2} 3x-\mathop{\lim }\limits_{x\to 2} 4\] \[\mathop{\lim }\limits_{x\to 2} x^{2} +\mathop{\lim }\limits_{x\to 2} 3x-\mathop{\lim }\limits_{x\to 2} 4=2^{2} +3*2-4=6\]Приведенные выше теоремы справедливы также и при:
\[x\to -\infty ,x\to a-0,x\to a+0,x\to a\]Возникают ситуации, когда для применения теорем необходимо сначала тождественно преобразовать функцию. Так, возникает, например, при нахождении предела дроби, знаменатель которой стремится к нулю.
Найти предел
\[\mathop{\lim }\limits_{x\to 2} \frac{x^{2} -x-2}{x^{2} -2x} \]Решение:
Применить теорему 5 нельзя, поскольку числитель и знаменатель функции равны 0. Возникает неопределенность.
\[\mathop{\lim }\limits_{x\to 2} \frac{x^{2} -x-2}{x^{2} -2x} =\frac{4-2-2}{4-4} =\left\langle \frac{0}{0} \right\rangle \]Поэтому необходимо выполнить преобразования:
\[\mathop{\lim }\limits_{x\to 2} \frac{x^{2} -x-2}{x^{2} -2x} =\frac{(x-2)(x+1)}{x(x-2)} =\frac{(x+1)}{x} \] \[\mathop{\lim }\limits_{x\to 2} \frac{x^{2} -x-2}{x^{2} -2x} =\frac{(x+1)}{x} =\frac{2+1}{2} =1,5\]Даны три функции $\phi (x)$, f(x), g(x), удовлетворяющие неравенствам для больших значений x:
\[\phi (x)\le f(x)\le g(x)\]Если функции $\phi (x)$, g(x) имеют один и тот же предел при х>$\infty $, то и функция, заключенная между ними, имеет равный с ними предел.
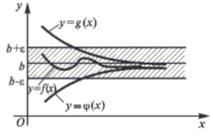
Рисунок 1. Сравнение функций
По рисунку 1 видно, что если функции $\phi (x)$, g(x) имеют при х>$\infty $, предел b, то при любом $\varepsilon $ $>$ 0, найдется такое число N, что функции окажутся внутри области, ограниченной прямыми b-$\varepsilon $ и b+$\varepsilon $. А функция, лежащая между ними, также является ограниченной данной областью.












