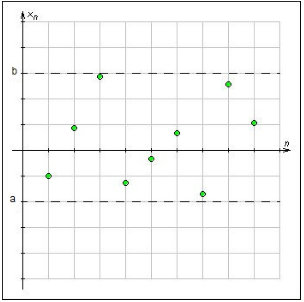
Последовательность \{an\}, n$\ \in $ N, называется ограниченной, если существуют числа a и b, при которых для каждого номера последовательности n справедливо неравенство (рис.1):
\[a\le a_{n} \le b\begin{array}{cc} {} & {a\ne b} \end{array}\]Например, последовательность вида:
\[a_{n} =\frac{1}{n^{2} } \] \[\frac{1}{n^{2} } =\frac{1}{1^{2} } ,\frac{1}{2^{2} } ,\frac{1}{3^{2} } ,\frac{1}{4^{2} } ...=1,\frac{1}{4} ,\frac{1}{9} ,\frac{1}{16} ...\]Ограничена, т.к. $0\le a_{n} \le 1$
Последовательность $a_n$, n$\ \in $ N, называется ограниченной сверху, если существует b, при котором для каждого номера последовательности n справедливо неравенство:
\[a_{n} \le b\]Например, последовательность вида:
\[a_{n} =100-n^{2} \] \[100-n^{2} =100-1,100-4,...=99,96...\]Ограничена сверху, т.к. $a_{n} \le 99$
Ограничение последовательности">
Рисунок 1. Ограничение последовательности
Последовательность $a_n$, n$\ \in $ N, называется ограниченной снизу, если существует а, при котором для каждого номера последовательности n справедливо неравенство:
\[a_{n} \ge a\]Например, последовательность вида:
\[a_{n} =n^{3} -2\] \[n^{3} -2=-1,6,25...\]Ограничена снизу, т.к. $a_{n} \ge -1$
Числовые последовательности могут быть неограниченными или постоянными.
Определить вид последовательности:
\[a_{n} =\left(-1\right)^{n} \cdot n\]Решение:
\[\left(-1\right)^{n} \cdot n=-1,2,-3,4...\]Не является ограниченной, т.к. для любых a и b можно найти большее или меньшее значение.
Определить вид последовательности:
\[a_{n} =4\]Решение:
\[4=4,4,4...\]Поскольку все члены последовательности равны, числовая последовательность -- постоянная.
Определить ограниченность последовательности
\[a_{n} =\frac{5n-2}{n+1} \]Решение:
\[a_{n} =\frac{5n-2}{n+1} =5-\frac{7}{n+1} \] \[a_{n} =\frac{3}{2} ,\frac{7}{3} ,\frac{13}{4} ...\]Вывод: Функция ограничена и сверху, и снизу, поскольку $a_{n} \ge \frac{3}{2} $ и $a_{n}
