Предел и его обозначение
Предел функции как один из важнейших разделов математического анализа определяет предельное значение функции, т.е. такое значение, после достижения которого функция уже не существует.
Разберем обозначение «предела»:
- Знак предела lim;
- $x\to a$ - это стремление х к определенной точке или бесконечности ($x\to \infty $)
- $f(x)=b$ - функция
Среди данных обозначений х является числовой переменной, которая изменяется на области Х (координатной плоскости оХ и оY). Рассмотрим график простейшей функции на рис.1. Оси графика образуют область ее изменения и говорят, что функция $y=x^{2} $ определена на множестве Х. Кроме числовой независимой переменной х, каждая функция имеет зависимую от х переменную y (иначе говоря, частное решение в конкретной точке).
Совокупность всех значений зависимой переменной составляет множество значений функции. На графике множество значений можно определить по оси оY, а область определений по оХ. Для рассматриваемого графика, область значений определяется как [0; $\infty $], а область определений [-$\infty $; $\infty $].
«Стремление» х означает последовательное приближение к числу а (предельной точки области Х или бесконечности) путем перебора максимально близких к нему значений.
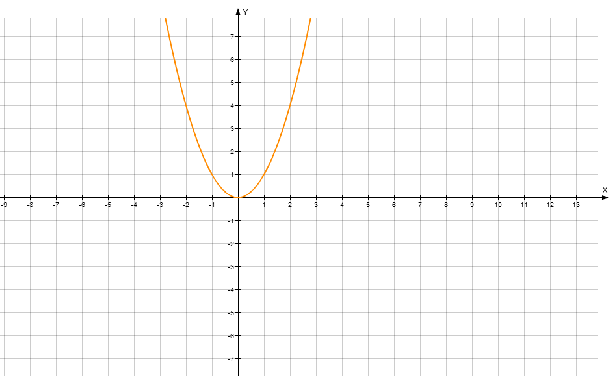
Рисунок 1. Функция $x^{2} $
Рассмотрим следующее выражение:
Его «чтение» должно производиться следующим образом: «Предел функции х + 4 при стремлении х к бесконечности»
Пределом является число b, к которому стремится функция, при стремлении x к а.
Проще говоря, к какому числу приблизится функция, при стремлении ее неизвестной к а.
Непрерывная функция
Функцию, которая имеет предел в точке a, называют непрерывной в этой точке.
\[\mathop{\lim }\limits_{x\to a} f(x)=f(a)\]Рассмотрим условия непрерывности функции:
- Функция должна быть определена, т.е. существует f(a);
- Предел функции в точке а -- существует;
- Предел функции в точке х = а равен значению функции в этой точке
Если функция y = f(x) непрерывна в каждой точке некоторого промежутка, то её называют непрерывной на данном промежутке.
Теоремы непрерывности функции
Если функции f(x) и g(x) непрерывны в точке х = а, то в этой точке непрерывны и такие функции, как:
- f(x) + g(x),
- f(x) -- g(x),
- f(x) • g(x).
Если функции f(x) и g(x) непрерывны в точке х = а и g(а) ≠ 0, то в точке х = а будет непрерывной также и функция f(x)/g(x).
Непрерывными являются функции вида:
- Многочлены \[y=a_{0} +a_{1} x+...+a_{n} x^{n} \]
- Дробно-рациональные функции (кроме нулей знаменателя) \[y=\frac{a_{0} +a_{1} x+a_{2} x^{2} ...+a_{n} x^{n} }{b_{0} +b_{1} x+b_{2} x^{2} ...+b_{m} x^{m} } \]
- Тригонометрические функции
- Показательные и логарифмические функции, а также модуль \[y=a^{x} y=\log _{a} x y=\sqrt[{n}]{x} y=\left|x\right|\]
$у = sin(x), y = cos(x), y = tg(x), y = ctg(x)$
$у = arcsin(x), y = arccos(x), y = arctg(x), y = arcctg(x)$
Примеры непрерывных функций:
- $y=x^{2} +4x-5$
- $y=\frac{x^{2} -2}{x-3} $ (кроме точки 3)
- $y=\sqrt[{4}]{x} $
Является ли сумма непрерывной, если обе функции непрерывны в точке в точке х = а?
\[\mathop{\lim }\limits_{x\to a} 5^{E} +\mathop{\lim }\limits_{x\to a} \log _{2} x\]Ответ: по теореме 1 функция непрерывна
Проверка функций на неопределенность проводится методом подстановки а вместо х, НО полученное значение предела у НЕПРЕРЫВНОЙ функции всегда равно числу а.
Является ли функция непрерывной?
\[\mathop{\lim }\limits_{x\to 1} 2E^{5} +4E-5\]Решение:
\[\mathop{\lim }\limits_{x\to 1} 2E^{5} +4E-5=2*1^{5} +4*1-5=2+4-5=1\]$1 = 1$
Вывод: функция непрерывна в точке 1











