Понятие пирамиды
Геометрическая фигура, образованная многоугольником и точкой, не лежащей в плоскости, содержащей этот многоугольник, соединенной со всеми вершинами многоугольника называется пирамидой (рис. 1).
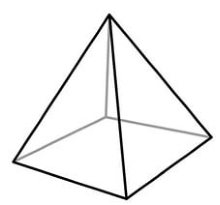
Многоугольник, из которого составлена пирамида, называется основанием пирамиды, получаемые при соединение с точкой треугольники - боковыми гранями пирамиды, стороны треугольников -- сторонами пирамиды, а общая для всех треугольников точка-- вершиной пирамиды.
Виды пирамид
В зависимости от количества углов в основании пирамиды ее можно назвать треугольной, четырехугольной и так далее (рис. 2).
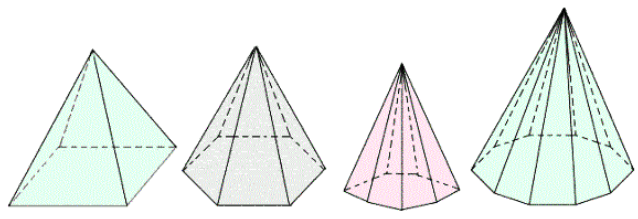
Рисунок 2.
Еще один вид пирамид -- правильная пирамида.
Пирамида, в основании которой лежит правильный многоугольник и высота пирамиды падает в его центр называется правильной пирамидой (рис. 3).
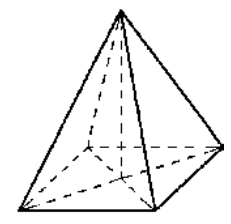
Рисунок 3. Правильная пирамида
Введем и докажем свойство правильной пирамиды.
Все боковые грани правильной пирамиды являются равнобедренными треугольниками, которые равны между собой.
Доказательство.
Рассмотрим правильную $n-$угольную пирамиду с вершиной $S$ высотой $h=SO$. Опишем вокруг основания окружность (рис. 4).
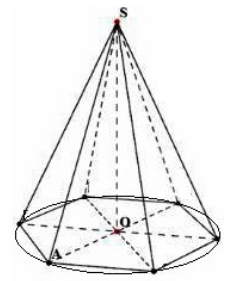
Рисунок 4.
Рассмотрим треугольник $SOA$. По теореме Пифагора, получим
\[AS=\sqrt{{AO}^2+{SO}^2}=\sqrt{R^2+h^2}\]Очевидно, что так будет определяться любое боковое ребро. Следовательно, все боковые ребра равны между собой, то есть все боковые грани -- равнобедренные треугольники. Докажем, что они равны между собой. Так как основание -- правильный многоугольник, то основания всех боковых граней равны между собой. Следовательно, все боковые грани равны по III признаку равенства треугольников.
Теорема доказана.
Введем теперь следующее определение, связанное с понятием правильной пирамиды.
Апофемой правильной пирамиды называется высота её боковой грани.
Очевидно, что по теореме один все апофемы равны между собой.
Площадь боковой поверхности правильной пирамиды определяется как произведение полупериметра основания на апофему.
Доказательство.
Обозначим сторону основания $n-$угольной пирамиды через $a$, а апофему через $d$. Следовательно, площадь боковой грани равна
\[s=\frac{1}{2}ad\]Так как, по теореме 1, все боковые стороны равны, то
\[S_{бок}=\frac{1}{2}and=\frac{P_{осн}}{2}d\]Теорема доказана.
Еще один вид пирамиды -- усеченная пирамида.
Если через обычную пирамиду провести плоскость, параллельную её основанию, то фигура, образованная между этой плоскостью и плоскостью основания называется усеченной пирамидой (рис. 5).
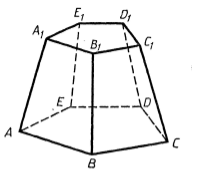
Рисунок 5. Усеченная пирамида
Боковыми гранями усеченной пирамиды являются трапеции.
Площадь боковой поверхности правильной усеченной пирамиды определяется как произведение суммы полупериметров оснований на апофему.
Доказательство.
Обозначим стороны оснований $n-$угольной пирамиды через $a\ и\ b$ соответственно, а апофему через $d$. Следовательно, площадь боковой грани равна
\[s=\frac{1}{2}(a+b)d\]Так как все боковые стороны равны, то
\[S_{бок}=\frac{1}{2}(a+b)nd=\frac{\sum{P_{осн}}}{2}d\]Теорема доказана.
Пример задачи
Найти площадь боковой поверхности усеченной треугольной пирамиды, если она получена из правильной пирамиды со стороной основания 4 и апофемой 5 путем отсечения плоскостью, проходящей через среднюю линию боковых граней.
Решение.
По теореме о средней линии получим, что верхнее основание усеченной пирамиды равно $4\cdot \frac{1}{2}=2$, а апофема равна $5\cdot \frac{1}{2}=2,5$.
Тогда, по теореме 3, получим
\[S_{бок}=\frac{1}{2}\left(12+6\right)\cdot \frac{5}{2}=\frac{90}{4}=22,5\]Ответ: $22,5$.











