В теории дифференцирования рассматривается задача нахождения производной функции, т.е. функции для которой $f(x)=F'(x)$.
В теории интегрирования рассматривается обратная задача, т.е. нахождение функции $F(x)$ для которой $F'(x)=f(x)$.
Первообразная $F(x)$ для функции $y=f(x)$ на отрезке $[a;b]$ - это функция, которая является дифференцируемой в каждой точке этого отрезка и для ее производной выполняется следующее равенство:
\[F'(x)=f(x).\]Равенство из определения 1 можно записать с помощью дифференциалов следующим образом:
$\frac{dF}{dx} =f(x)$ или $dF=f(x)dx$.
Для нахождения первообразной некоторой функции можно пользоваться таблицей производных.
Вычислить первообразную $F(x)$ заданных функций:
1) $f(x)=x^{2} $; 2) $f(x)=\cos x$.
Решение:
1) Первообразной функции $f(x)=x^{2} $ является функция $F(x)=\frac{x^{3} }{3} $, так как
\[F'(x)=\left(\frac{x^{3} }{3} \right)'=\frac{3x^{2} }{3} =x^{2} =f(x).\]2) Первообразной функции $f(x)=\cos x$ является функция $F(x)=\sin x$, так как
\[F'(x)=\left(\sin x\right)'=\cos x=f(x).\]Первообразная $F(x)$ функции $f(x)$ имеет конечную производную, что означает, что первообразная $F(x)$ является функцией непрерывной.
Если функция $F(x)$ - это первообразная для функции $y=f(x)$ на некотором отрезке $[a;b]$, то и функция вида $\Phi (x)=F(x)+C$ также является первообразной для исходной функции, при этом $C=const$.
Теорема 1 показывает, что множество полученных первообразных функций для заданной функции является бесконечным.
Определить множество первообразных $F(x)$ для заданных функций:
1) $f(x)=\frac{1}{x} $; 2) $f(x)=\sin x$.
Решение:
1) Первообразными функции $f(x)=\frac{1}{x} $ является множество функций $F(x)=\ln |x|+C$, так как
\[F'(x)=\left(\ln |x|+C\right)'=\frac{1}{x} =f(x).\]2) Первообразными функции $f(x)=\sin x$ является множество функций $F(x)=-\cos x+C$, так как
\[F'(x)=\left(-\cos x+C\right)'=\sin x=f(x).\]Если $F_{1} (x)$ и $F_{2} (x)$ - две первообразные от одной заданной функции $y=f(x)$ на отрезке $[a;b]$, то разность между ними равна некоторому постоянному числу, т.е.
\[F_{1} (x)-F_{2} (x)=C=const.\]Теорему 2 можно перефразировать следующим образом: каждая функция, являющаяся первообразной для заданной функции $f(x)$, может быть записана в виде $F(x)+C$.
Вычислить несколько первообразных $F(x)$ для заданной функции: $f(x)=x$.
Решение:
Первообразными функции $f(x)=x$ является множество функций $F(x)=\frac{x^{2} }{2} +C$, так как
\[F'(x)=\left(\frac{x^{2} }{2} +C\right)'=\frac{2x}{2} =x=f(x).\]Выпишем две первообразные:
1) $F(x)=\frac{x^{2} }{2} +2$; 2) $F(x)=\frac{x^{2} }{2} +10$.
Каждая функция $y=f(x)$, непрерывная на отрезке $[a;b]$, имеет на данном отрезке первообразную $F(x)$.
Совокупность всех первообразных заданной функции $y=f(x)$, определенной на некотором отрезке, называется неопределенным интегралом от заданной функции $y=f(x)$. Неопределенный интеграл обозначается символом $\int f(x)dx $.
Определение 2 можно записать следующим образом:
\[\int f(x)dx =F(x)+C.\]Обозначения:
- $\int $ - знак интеграла;
- $f (x) $ - подынтегральная функция;
- $f(x)dx$ - подынтегральное выражение;
- $x$ - переменная интегрирования.
Интегрирование функции $y=f(x)$ -- это операция нахождения первообразной заданной функции $y=f(x)$ или неопределенного интеграла от заданной функции $y=f(x)$.
Операция интегрирования является обратной для операции дифференцирования.
Геометрический смысл: неопределенный интеграл представляет собой семейство параллельно расположенных кривых $F(x)+C$, где каждому конкретному числовому значению постоянной $C$ соответствует определенная кривая из указанного семейства (рис.1).

Рис. 1
График каждой кривой из семейства первообразных называется интегральной кривой.
Найти неопределенный интеграл от заданной функции $f(x)=2$ и изобразить некоторые кривые на координатной плоскости.
Решение:
Для функции $f(x)=2$ неопределенный интеграл имеет вид:
\[\int 2dx =2x+C.\]Выпишем интегралы для разных значений константы:
1) $\int 2dx =2x$; 2) $\int 2dx =2x+1$; 3) $\int 2dx =2x+2$.
Изобразим полученные кривые на координатной плоскости (рис.2).
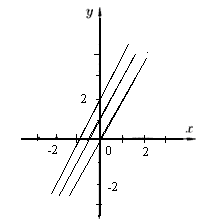
Найти неопределенный интеграл от заданных функций:
1) $f(x)=x$; 2) $f(x)=\sin x$.
Решение:
1) Для функции $f(x)=x$ неопределенный интеграл имеет вид:
\[\int xdx =\frac{x^{2} }{2} +C.\]2) Для функции $f(x)=\sin x$ неопределенный интеграл имеет вид:
\[\int \sin xdx =-\cos x+C.\]










