Понятие перпендикулярных плоскостей
При пересечении двух плоскостей у нас получается $4$ двугранных угла. Два угла равны $\varphi $, а два другие равны ${180}^0-\varphi $.
Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.
Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен $90^\circ$ (рис. 1).
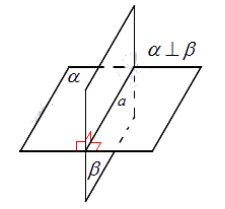
Рисунок 1. Перпендикулярные плоскости
Признак перпендикулярности двух плоскостей
Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.
Доказательство.
Пусть нам даны плоскости $\alpha $ и $\beta $, которые пересекаются по прямой $AC$. Пусть прямая $AB$, лежащая в плоскости $\alpha $ перпендикулярна плоскости $\beta $ (рис. 2).
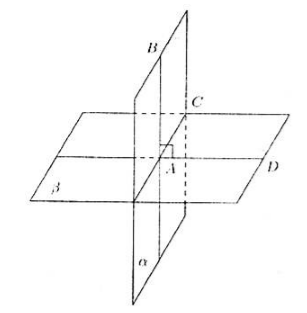
Рисунок 2.
Так как прямая $AB$ перпендикулярна плоскости $\beta $, то она перпендикулярна и прямой $AC$. Проведем дополнительно прямую $AD$ в плоскости $\beta $, перпендикулярно прямой $AC$.
Получаем, что угол $BAD$ - линейный угол двугранного угла, равный $90^\circ$. То есть, по определению 1, угол между плоскостями равен $90^\circ$, значит, данные плоскости перпендикулярны.
Теорема доказана.
Из этой теоремы следует следующая теорема.
Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.
Доказательство.
Пусть нам даны две плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Плоскость $\gamma $ перпендикулярна прямой $c$ (рис. 3)
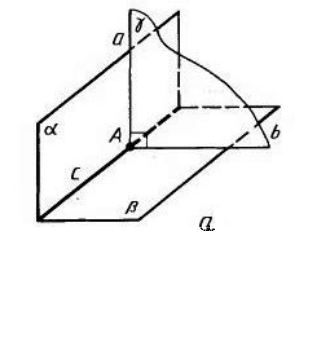
Рисунок 3.
Так как прямая $c$ принадлежит плоскости $\alpha $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\alpha $ и $\gamma $ перпендикулярны.
Так как прямая $c$ принадлежит плоскости $\beta $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\beta $ и $\gamma $ перпендикулярны.
Теорема доказана.
Для каждой из этих теорем справедливы и обратные утверждения.
Примеры задач
Пусть нам дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Найти все пары перпендикулярных плоскостей (рис. 5).
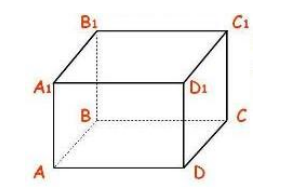
Рисунок 4.
Решение.
По определению прямоугольного параллелепипеда и перпендикулярных плоскостей видим следующие восемь пар перпендикулярных между собой плоскостей: $(ABB_1)$ и $(ADD_1)$, $(ABB_1)$ и $(A_1B_1C_1)$, $(ABB_1)$ и $(BCC_1)$, $(ABB_1)$ и $(ABC)$, $(DCC_1)$ и $(ADD_1)$, $(DCC_1)$ и $(A_1B_1C_1)$, $(DCC_1)$ и $(BCC_1)$, $(DCC_1)$ и $(ABC)$.
Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.
Доказательство.
Пусть нам даны перпендикулярные плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Из точки $A$ плоскости $\beta $ проведен перпендикуляр $AC$ к плоскости $\alpha $. Предположим, что $AC$ не лежит в плоскости $\beta $ (рис. 6).
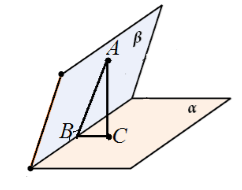
Рисунок 5.
Рассмотрим треугольник $ABC$. Он является прямоугольным с прямым углом $ACB$. Следовательно, $\angle ABC\ne {90}^0$.
Но, с другой стороны, $\angle ABC$ является линейным углом двугранного угла, образованного этими плоскостями. То есть двугранный угол, образованный этими плоскостями не равняется 90 градусам. Получаем, что угол между плоскостями не равен $90^\circ$. Противоречие. Следовательно, $AC$ лежит в плоскости $\beta $.
ч. т. д.











