Сначала рассмотрим разницу между понятиями признак, свойство и аксиома.
Признаком называют некий факт, по которому можно определить истинность суждения об интересующем объекте.
Прямые являются параллельными, если их секущая образует равные накрест лежащие углы.
Свойство формулируется в том случае, когда есть уверенность в справедливости суждения.
Аксиомой называют такое утверждение, которое не требует доказательства и принимается как истина без него.
Каждая наука имеет аксиомы, на которых строятся последующие суждения и их доказательства.
Аксиома параллельных прямых
Иногда аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.
Через точку, которая не лежит на заданной прямой, на плоскости можно провести лишь одну прямую, которая будет параллельной заданной.
Аксиома доказательства не требует.
Свойства параллельных прямых
Свойство1. Свойство транзитивности параллельности прямых:
Когда одна из двух параллельных прямых является параллельной третьей, то и вторая прямая будет ей параллельна.
Свойства требуют доказательств.
Доказательство:
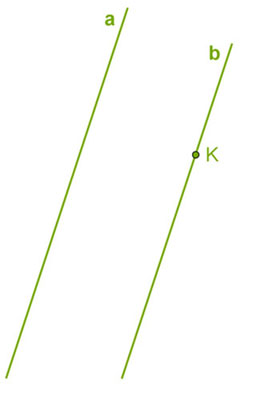
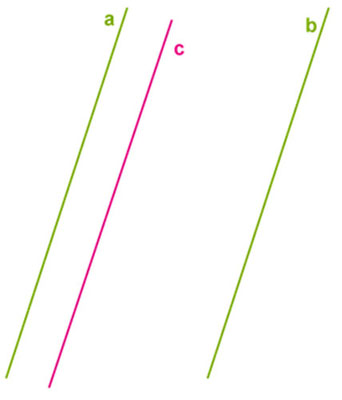
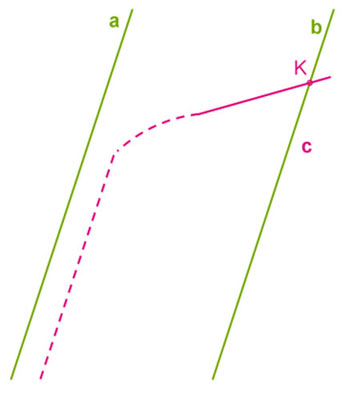
Пусть имеются две параллельные прямые $a$ и $b$. Прямая $с$ параллельна прямой $а$. Проверим, будет ли в таком случае прямая $с$ параллельна и прямой $b$.
Для доказательства будем пользоваться противоположным суждением:
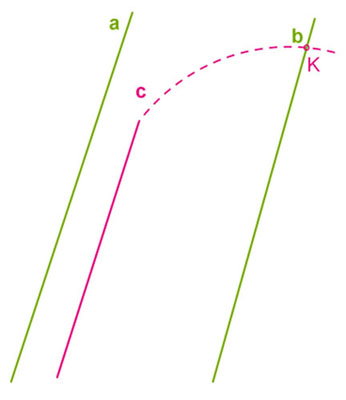
Представим, что возможен такой вариант, при котором прямая $c$ параллельна одной из прямых, например, прямой $a$, а другую – прямую $b$ – пересекает в некоторой точке $K$.
Получаем противоречие согласно аксиоме параллельных прямых. Получается ситуация, при которой в одной точке пересекаются две прямые, к тому же параллельные одной и той же прямой $a$. Такая ситуация невозможна, следовательно, прямые $b$ и $c$ пересекаться не могут.
Таким образом, доказано, что если одна из двух параллельных прямых является параллельной третьей прямой, то и вторая прямая параллельна третьей прямой.
Свойство 2.
Если одна из двух параллельных прямых пересекается третьей, то ею будет пересекаться и вторая прямая.
Доказательство:
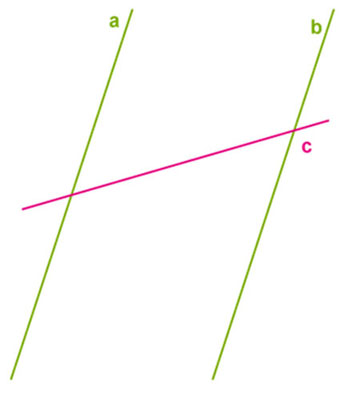
Пусть имеются две параллельные прямые $а$ и $b$. Также пусть имеется некоторая прямая $с$, которая пересекает одну из параллельных прямых, например, прямую $а$. Необходимо показать, что прямая $с$ пересекает и вторую прямую – прямую $b$.
Построим доказательство методом от противного.
Представим, что прямая $с$ не пересекает прямую $b$. Тогда через точку $К$ проходят две прямые $а$ и $с$, которые не пересекают прямую $b$, т. е. являются параллельными ей. Но такая ситуация противоречит аксиоме параллельных прямых. Значит, предположение было неверным и прямая $с$ пересечет прямую $b$.
Теорема доказана.
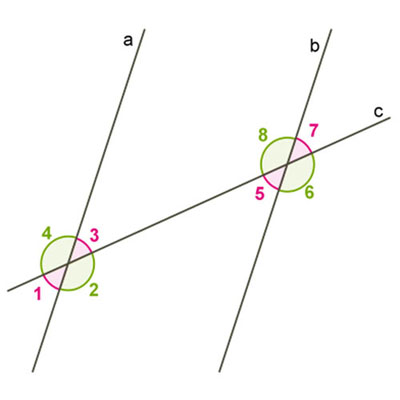
Свойства углов, которые образуют две параллельные прямые и секущая: накрест лежащие углы равны, соответственные углы равны, * сумма односторонних углов равна $180^{\circ}$.
Даны две параллельные прямые и третья прямая, перпендикулярная одно из них. Доказать, что эта прямая перпендикулярна и другой из параллельных прямых.
Доказательство.
Пусть имеем прямые $а \parallel b$ и $с \perp а$.
Поскольку прямая $с$ пересекает прямую $а$, то согласно свойству параллельных прямых она будет пересекать и прямую $b$.
Секущая $с$, пересекая параллельные прямые $а$ и $b$, образует с ними равные внутренние накрест лежащие углы.
Т.к. $с \perp а$, то углы будут по $90^{\circ}$.
Следовательно, $с \perp b$.
Доказательство завершено.