Любой квадратной матрице $A=\left(a_{ij} \right)_{n\times n} $ можно сопоставить некоторое число, которое будем называть определителем данной матрицы (детерминант).
Для обозначения определителя матрицы используют следующие символы: $|A|,\, \Delta $ или $\det A$.
В зависимости от порядка матрицы различают несколько способов вычисления определителя.
Определитель матрицы 2-го порядка можно вычислить по формуле:
Дана матрица $A=\left(\begin{array}{cc} {1} & {-2} \\ {3} & {1} \end{array}\right)$. Найти определитель.
Решение:
\[\det A=\left|\begin{array}{cc} {1} & {-2} \\ {3} & {1} \end{array}\right|=1\cdot 1-3\cdot (-2)=1+6=7\]Для нахождения определителя матрицы 3-го порядка можно использовать одно из двух правил:
- правило треугольника;
- правило Саррюса.
Определитель матрицы 3-го порядка с помощью правила треугольника вычисляется по формуле:
\[\left|\begin{array}{ccc} {a_{11} } & {a_{12} } & {a_{13} } \\ {a_{21} } & {a_{22} } & {a_{23} } \\ {a_{31} } & {a_{32} } & {a_{33} } \end{array}\right|=\] \[=a_{11} \cdot a_{22} \cdot a_{33} +a_{31} \cdot a_{12} \cdot a_{23} +a_{21} \cdot a_{32} \cdot a_{13} -a_{31} \cdot a_{22} \cdot a_{13} -a_{21} \cdot a_{12} \cdot a_{33} -a_{11} \cdot a_{23} \cdot a_{32} \]Для лучшего запоминания правила треугольника можно пользоваться следующей схемой:
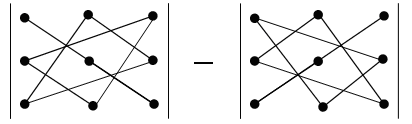
Дана матрица $A=\left(\begin{array}{ccc} {1} & {3} & {4} \\ {0} & {2} & {1} \\ {1} & {5} & {-1} \end{array}\right)$. Найти определитель.
Решение:
\[\begin{array}{l} {\det A=\left|\begin{array}{ccc} {1} & {3} & {4} \\ {0} & {2} & {1} \\ {1} & {5} & {-1} \end{array}\right|=1\cdot 2\cdot (-1)+1\cdot 3\cdot 1+4\cdot 0\cdot 5-1\cdot 2\cdot 4-0\cdot 3\cdot (-1)-5\cdot 1\cdot 1=} \\ {=-2+3+0-8-0-5=-12} \end{array}\]Для вычисления определителя по правилу Саррюса необходимо выполнить следующие действия:
- дописать слева от определителя для первых столбца;
- перемножить элементы, расположенные на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы побочной диагонали и параллельных ей диагоналей, взяв произведения со знаком «-»
Для лучшего запоминания правила треугольника можно пользоваться следующей схемой:
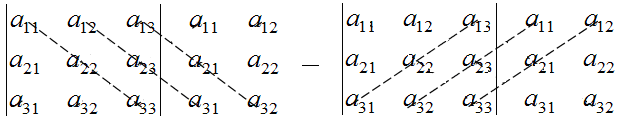
Дана матрица $A=\left(\begin{array}{ccc} {1} & {3} & {4} \\ {0} & {2} & {1} \\ {-2} & {5} & {-1} \end{array}\right)$. Найти определитель.
Решение:
\[\begin{array}{l} {A=\left|\begin{array}{ccc} {1} & {3} & {4} \\ {0} & {2} & {1} \\ {-2} & {5} & {-1} \end{array}\right|\, \, \, \begin{array}{c} {1} \\ {0} \\ {-2} \end{array}\, \, \, \, \begin{array}{c} {3} \\ {2} \\ {5} \end{array}=1\cdot 2\cdot (-1)+3\cdot 1\cdot (-2)+4\cdot 0\cdot 5-4\cdot 2\cdot (-2)-1\cdot 1\cdot 5-3\cdot 0\cdot (-1)=} \\ {=-2-6+0+16-5-0=3} \end{array}\]Для вычисления определителя матрицы 4-го порядка и выше можно использовать один из двух способов:
- разложение по элементам строки;
- разложение по элементам столбца.
Данные способы сводят вычисление определителя порядка $n$ к вычислению определителя порядка $n-1$ за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение определителя матрицы по элементам строки в общем виде можно записать по формуле:
\[\det A=a_{i1} \cdot A_{i1} +a_{i2} \cdot A_{i2} +...+a_{in} \cdot A_{in} \]Разложение определителя матрицы по элементам столбца в общем виде можно записать по формуле:
\[\det A=a_{1j} \cdot A_{1j} +a_{2j} \cdot A_{2j} +...+a_{nj} \cdot A_{nj} \]При разложении определителя по элементам строки (столбца) желательно выбирать строку (столбец), в которой(-ом) есть нули.
Дана матрица $A=\left(\begin{array}{cccc} {0} & {1} & {-1} & {3} \\ {2} & {1} & {0} & {0} \\ {-2} & {4} & {5} & {1} \\ {3} & {2} & {1} & {0} \end{array}\right)$. Записать разложение определителя по произвольной строке (столбцу).
Решение:
- разложение по второй строке: \[A=\left|\begin{array}{cccc} {0} & {1} & {-1} & {3} \\ {2} & {1} & {0} & {0} \\ {-2} & {4} & {5} & {1} \\ {3} & {2} & {1} & {0} \end{array}\right|=2\cdot (-1)^{3} \cdot \left|\begin{array}{ccc} {1} & {-1} & {3} \\ {4} & {5} & {1} \\ {2} & {1} & {0} \end{array}\right|+1\cdot (-1)^{4} \cdot \left|\begin{array}{ccc} {0} & {-1} & {3} \\ {-2} & {5} & {1} \\ {3} & {1} & {0} \end{array}\right|=-2\cdot \left|\begin{array}{ccc} {1} & {-1} & {3} \\ {4} & {5} & {1} \\ {2} & {1} & {0} \end{array}\right|+1\cdot \left|\begin{array}{ccc} {0} & {-1} & {3} \\ {-2} & {5} & {1} \\ {3} & {1} & {0} \end{array}\right|\]
- разложение по четвертому столбцу: \[A=\left|\begin{array}{cccc} {0} & {1} & {-1} & {3} \\ {2} & {1} & {0} & {0} \\ {-2} & {4} & {5} & {1} \\ {3} & {2} & {1} & {0} \end{array}\right|=3\cdot (-1)^{5} \cdot \left|\begin{array}{ccc} {2} & {1} & {0} \\ {-2} & {4} & {5} \\ {3} & {2} & {1} \end{array}\right|+1\cdot (-1)^{7} \cdot \left|\begin{array}{ccc} {0} & {1} & {-1} \\ {2} & {1} & {0} \\ {3} & {2} & {1} \end{array}\right|=-3\cdot \left|\begin{array}{ccc} {2} & {1} & {0} \\ {-2} & {4} & {5} \\ {3} & {2} & {1} \end{array}\right|-1\cdot \left|\begin{array}{ccc} {0} & {1} & {-1} \\ {2} & {1} & {0} \\ {3} & {2} & {1} \end{array}\right|\]
Свойства определителя:
- элементарные преобразования строк (столбцов) матрицы не меняют значения определителя;
- перестановка строк (столбцов) меняет знак определителя на противоположный (c «+» на «-» и наоборот);
- определитель треугольной матрицы находится как произведение элементов, которые расположены на главной диагонали.
Дана матрица $A=\left(\begin{array}{ccc} {1} & {3} & {4} \\ {0} & {2} & {1} \\ {0} & {0} & {5} \end{array}\right)$. Найти определитель.
Решение:
\[\det A=\left|\begin{array}{ccc} {1} & {3} & {4} \\ {0} & {2} & {1} \\ {0} & {0} & {5} \end{array}\right|=1\cdot 2\cdot 5=10\]Определитель матрицы, содержащей нулевую строку, равен нулю.
Определитель матрицы, содержащей нулевой столбец, равен нулю.












