Операции сложения и вычитания выполняются для чисел, представленных в алгебраической форме.
Суммой двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством
Другими словами, суммой двух заданных комплексных чисел является комплексное число, действительная и мнимая части которого определяется как сумма соответственно действительных и мнимых частей исходных слагаемых.
Сумму любого количества заданных комплексных чисел можно найти путем суммирования действительных частей и суммирования мнимых частей слагаемых.
Для операции суммы комплексных чисел справедливо следующее правило: (от перестановки слагаемых сумма не меняется).
Сумму двух заданных комплексных чисел можно найти с помощью комплексной плоскости по правилу «параллелограмма» (правило параллелограмма сложения векторов).
Иллюстрация примера сложения комплексных чисел с использованием комплексной плоскости приведена на рис.1-2.
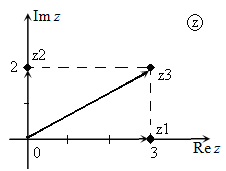
Рис. 1
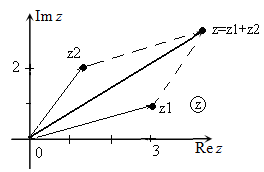
Рис. 2
Найти сумму $z_{1} +z_{2} $ для комплексных чисел:
1) $z_{1} =3+2i$ и $z_{2} =1-2i$; 2) $z_{1} =3$ и $z_{2} =1+5i$; 3) $z_{1} =3+9i$ и $z_{2} =-7i$.
Решение:
Для сложения комплексных чисел воспользуемся определением и получим:
1) $z_{1} +z_{2} =(3+2i)+(1-2i)=(3+1)+(2-2)i=4+0\cdot i=4$
2) $z_{1} +z_{2} =(3+0\cdot i)+(1+5i)=(3+1)+(0+5)i=4+5i$
3) $z_{1} +z_{2} =(3+9i)+(0-7i)=(3+0)+(9-7)i=3+2i$
Найти модуль суммы $|z_{1} +z_{2} |$ двух заданных комплексных чисел:
1) $z_{1} =1+2i$ и $z_{2} =1-5i$; 2) $z_{1} =\sqrt{3} $ и $z_{2} =\sqrt{5} i$; 3) $z_{1} =\sqrt{3} +9i$ и $z_{2} =-7i$.
Решение:
Для сложения комплексных чисел воспользуемся определением. Для вычисления модуля комплексного числа воспользуемся формулой:
1) Для чисел $z_{1} =1+2i$ и $z_{2} =1-5i$ получим:
2) Для чисел $z_{1} =\sqrt{3} $ и $z_{2} =\sqrt{5} i$ получим:
3) Для чисел $z_{1} =\sqrt{3} +9i$ и $z_{2} =-7i$ получим:
Разностью двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством
Модуль разности двух заданных комплексных чисел равен расстоянию между точками, которые изображают эти числа на комплексной плоскости:
Найти разность $z_{1} -z_{2} $ для комплексных чисел:
1) $z_{1} =3+2i$ и $z_{2} =1-2i$; 2) $z_{1} =3$ и $z_{2} =1+5i$; 3) $z_{1} =3+9i$ и $z_{2} =-7i$.
Решение:
Для нахождения разности комплексных чисел воспользуемся определением и получим:
1) $z_{1} -z_{2} =(3+2i)-(1-2i)=(3-1)+(2-(-2))i=2+4i$
2) $z_{1} -z_{2} =(3+0\cdot i)-(1+5i)=(3-1)+(0-5)i=2-5i$
3) $z_{1} -z_{2} =(3+9i)-(0-7i)=(3-0)+(9-(-7))i=3+16i$
Найти модуль разности двух заданных комплексных чисел:
1) $z_{1} =1+2i$ и $z_{2} =1-5i$; 2) $z_{1} =\sqrt{3} $ и $z_{2} =\sqrt{5} i$; 3) $z_{1} =\sqrt{3} +9i$ и $z_{2} =-7i$.
Решение:
Воспользуемся формулой из примечания 4.
1) Для чисел $z_{1} =1+2i$ и $z_{2} =1-5i$ получим:
2) Для чисел $z_{1} =\sqrt{3} $ и $z_{2} =\sqrt{5} i$ получим:
3) Для чисел $z_{1} =\sqrt{3} +9i$ и $z_{2} =-7i$ получим:
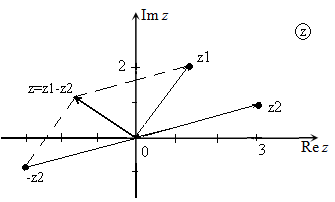
Рис. 3
На комплексной плоскости операцию вычитания можно реализовать, используя другой алгоритм:
- соединить точки, изображающие исходные комплексные числа;
- достроить параллелограмм;
- радиус-вектор, параллельный прямой, соединяющей точки, изображающие исходные комплексные числа, изображает разность исходных комплексных чисел - $z=z_{1} -z_{2} $.
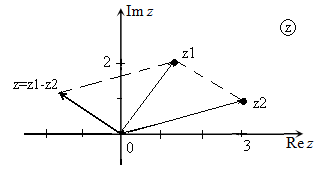
Рис. 4
Построить на комплексной плоскости сумму и разность изображенных на плоскости комплексных чисел (рис.5): $z_{1} +z_{2} ,z_{1} -z_{2} $.
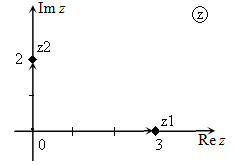
Рис. 5
Решение:
Для построения воспользуемся примечаниями 4 и 6.
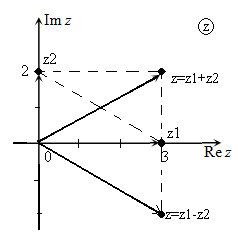
Рис. 6











