Извлечение корня из некоторого комплексного числа выполняется для чисел, которые представлены в тригонометрической форме.
Выражение вида $z=a+bi$, где $a$ и $b$ - вещественные числа, а $i$ - «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt{-1} $ или $i^{2} =-1$.
Запись некоторого комплексного числа $z$ в следующем виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ - модуль комплексного числа $z$, который определяется по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ - аргумент комплексного числа $z$, который определяется по формуле $\varphi =arctg\frac{b}{a} $.
Корень $n$-ой степени из некоторого комплексного числа $z$ - это такое комплексное число $w$, $n$-я степень которого равна $z$, то есть
Однозначно извлечь корень из некоторого комплексного числа невозможно, так как он имеет количество значений, равное его степени.
С геометрической точки зрения все значения корня $n$-ой степени из некоторого комплексного числа $z$ лежат на некоторой окружности радиуса $\sqrt[{n}]{z} $, центр которой находится в начале координат О(0;0), и образуют правильный $n$-угольник (рис. 1).
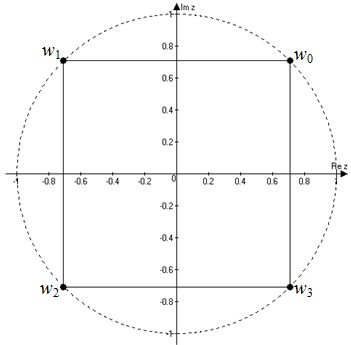
Рис. 1
Все комплексные числа, представленные в тригонометрической форме, можно возвести в некоторую степень по формуле Муавра:
Аналогично применяя формулу Муавра для вычисления корня $n$-ой степени из некоторого комплексного числа $z$ (не равного нулю) получаем:
Корнем $n$-й степени из некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
Если некоторое комплексное число $z$ отлично от нуля, то корень $n$-й степени существует всегда.
Выполнить действие $\sqrt[{3}]{z} $, где $z=2\cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi }{3} +i\cdot \sin \frac{\pi }{3} \right)$.
Для $k=1$ получаем: $w_{2} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi +2\pi }{3} +i\cdot \sin \frac{\pi +2\pi }{3} \right)=\sqrt[{3}]{2} \cdot \left(\cos \pi +i\cdot \sin \pi \right)$.
Для $k=2$ получаем: $w_{3} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi +4\pi }{3} +i\cdot \sin \frac{\pi +4\pi }{3} \right)=\sqrt[{3}]{2} \cdot \left(\cos \frac{5\pi }{3} +i\cdot \sin \frac{5\pi }{3} \right)$.
Запись некоторого комплексного числа $z$ в следующем виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ - вещественная (действительная) часть, обозначение $Rez=a$;
- $b$ - мнимая часть, обозначение $Imz=b$.
Чтобы извлечь корень $n$-ой степени из некоторого комплексного числа $z$, представленного в алгебраической форме, необходимо выполнить следующие действия:
- записать данное число в тригонометрической форме;
- извлечь корни, используя определение.
Чтобы комплексное число $z$, записанное в алгебраической форме, привести к тригонометрической форме записи, необходимо выполнить следующее:
- вычислить модуль и аргумент;
- подставить полученные значения в выражение $z=r(\cos \varphi +i\cdot \sin \varphi )$.
Выполнить операцию извлечения корня $\sqrt[{3}]{z} $ для заданных комплексных чисел в алгебраической форме представления:
Решение:
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.
По условию $a=\frac{1}{2} ,b=\frac{1}{2} $.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа, используя формулу (*):
Подставим полученные значения и получим:
Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =\sqrt[{3}]{z} =\sqrt[{3}]{\frac{\sqrt{2} }{2} } \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)$.
Для $k=1$ получаем:
Для $k=2$ получаем:
Запись комплексного числа $z$ в следующем виде $z=r\cdot e^{i\varphi } $ называется показательной формой записи, где число $r$ - модуль комплексного числа $z$, который определяется по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ - аргумент комплексного числа $z$, который определяется по формуле $\varphi =arctg\frac{b}{a} $.
Чтобы извлечь корень $n$-ой степени из некоторого комплексного числа $z$, представленного в показательной форме, необходимо выполнить следующие действия:
- записать число в тригонометрической форме;
- извлечь корни, используя определение.
Чтобы комплексное число $z$, записанное в показательной форме, привести к тригонометрической форме записи, необходимо выполнить следующее:
- определить из показательной записи числа значения модуля и аргумента;
- подставить полученные значения в выражение $z=r(\cos \varphi +i\cdot \sin \varphi )$.
Выполнить операцию извлечения корня $\sqrt{z} $ для заданных комплексных чисел в показательной форме представления:
Решение:
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.
Определим значения модуля и аргумента: $r=3,\, \, \varphi =\frac{\pi }{3} $.
Запись числа в тригонометрической форме имеет вид: $z=3\cdot (\cos \frac{\pi }{3} +i\sin \frac{\pi }{3} )$.
Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =\sqrt{z} =\sqrt{3} \cdot \left(\cos \frac{\pi }{6} +i\cdot \sin \frac{\pi }{6} \right)$.
Для $k=1$ получаем:












