Свойства функции распределения
Вначале напомним определение функции распределения вероятностей.
Функцией распределения называется функция $F(x)$ удовлетворяющая условию $F\left(x\right)=P(X
Введем свойства функции распределения:
1. Функция распределения является неубывающей функцией.
Доказательство: очевидно, что для любых событий $x_1 \[F\left(x_1\right)=P\left(Xч. т. д.
2. Существуют пределы ${\mathop{lim}_{x\to -\infty } F(x)\ }$ и ${\mathop{lim}_{x\to +\infty } F(x)\ }$, причем выполняются равенства:
Доказательство: Существование данных пределов следует из непрерывности и ограниченности функции $F(x)$. Докажем сначала, что:
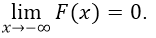
Рисунок 1.
Рассмотрим убывающую последовательность событий $A_n=(X
Лемма 1: Дана убывающая последовательность вложенных друг друга множеств ${\dots \subseteq A_n\subseteq A_{n-1}\subseteq \dots \subseteq A}_3\subseteq A_2\subseteq A_1$ удовлетворяющая условиям $A={\cap A}_n$ и $\mu \left(A_n\right)
Используя лемму 1, получим
Докажем теперь, что:
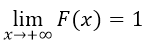
Рисунок 2.
Рассмотрим убывающую последовательность событий $B_n=(X\ge n)$, такую что$B_{n+1}=(X\ge (n+1))\subseteq B_n=(X\ge n)$ для всех $n\ge 1$. Очевидно, что пересечение всех событий $B_n$ $B={\cap B}_n=\emptyset $. Поэтому, по лемме 1, получим
ч. т. д.
3. $F(x)$ непрерывна слева любой точке, то есть:
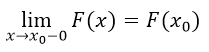
Рисунок 3.
Доказательство. Существование предела следует из непрерывности и ограниченности функции $F(x)$. Рассмотрим следующую разность $F\left(x_0\right)-F\left(x_0-\frac{1}{n}\right)$. Очевидно, что
Следовательно, $F\left(x_0\right)-F\left(x_0-\frac{1}{n}\right)\to 0$. То есть:
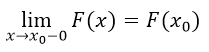
Рисунок 4.
ч. т. д.
4. Для любых $x_0$ выполняется равенство: $F\left(x_0+0\right)-F\left(x_0\right)=P({X=x}_0)$.
Это свойство очевидно.
5. Для любых $X$ выполняется равенство: $P\left(a\le X
Доказательство. Очевидно, что $\left(X \[F\left(a\right)+P\left(a\le Xч. т. д.
Если функция непрерывна во всех точках справа, то$P\left(a\le X\le b\right)=P\left(a
График функции распределения вероятностей
- Пусть случайная величина $X$ является дискретной. Тогда график функции распределения такой случайной величины всегда представляет собой ступенчатую функцию, скачки которой происходят в точках возможных значений случайной величины (рис. 1).
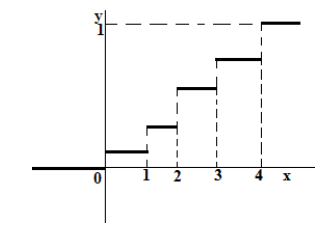
- Пусть случайная величина $X$ теперь является непрерывной. График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 2).
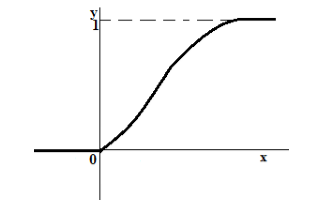
- Пусть случайная величина $X$ является смешанной. График функции распределения такой случайной величины всегда представляет собой неубывающую функцию, которая имеет минимальное значение в 0, максимальное значение в 1, но которая не на всей области определения является непрерывной функцией (имеет скачки в отдельных точках) (рис. 3).
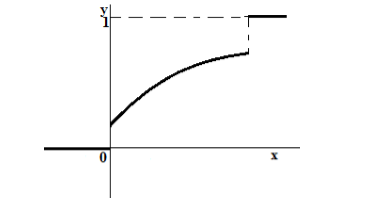
Рисунок 7. Функция распределения смешанной случайной величины
Примеры задач с использованием понятия функции распределения
Приведен ряд распределений появления события $A$ в трех опытах

Рисунок 8.
Найти функцию распределения вероятностей и построить её график.
Решение.
При $x\le 1$, $F\left(x\right)=0$;
При $1
При $2
При $x>3$, $F\left(x\right)=0,2+0,1+0,3+0,4=1$;
Отсюда получаем следующую функцию распределения вероятностей:
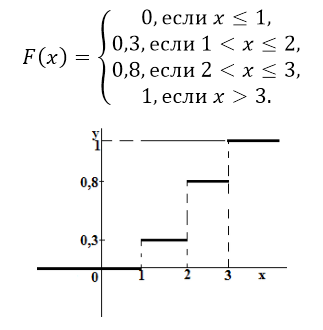
Рисунок 9.
Случайная величина задана следующей функцией распределения:
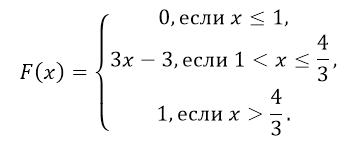
Рисунок 10.
Найти вероятность, что величина $X$ будет принадлежать интервалу $\left(\frac{7}{6};;1,2\right)$.
Решение. Нам необходимо найти значение $P\left(\frac{7}{6} \[P\left(\frac{7}{6}\le XОтвет: 0,1.











