Экстремумы функции
Для того чтобы ввести понятие возрастающих и убывающих функций, вначале познакомимся с таким понятием, как экстремумы функций. Это понятие нам будет необходимо не для самого определения таких функций, а для построения схемы нахождения таких промежутков для конкретно заданных функций.
Точка $x'$ входящая в область определения функции называется точкой экстремума, если она либо будет точкой максимума, либо будет точкой минимума для функции $f(x)$.
Точка $x'$ будет называться точкой максимума для введенной функции $f(x)$, если у она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\le f(x'{\rm \ })$.
Точка $x'$ будет называться точкой минимума для введенной функции $f(x)$, если она имеет такую окрестность, что для всех точек $x$, которые входят в эту окрестность, будет верно $f(x)\ge f(x'{\rm \ })$.
Чтобы полностью разобраться в данном понятии, далее введем понятие критической точки функции.
Точка $x'$ будет называться критической точкой для данной функции $f(x)$, если выполняются два следующих условия:
- Точка $x'$ является внутренней точкой для области определения данной функции;
- $f'\left(x'{\rm \ }\right)=0$ или не существует.
Сформулируем без доказательства теоремы о необходимом (теорема 1) и достаточном (теорема 2) условии для существования точки экстремума.
Если $y=f(x)$ имеет экстремум в точке $x_0$, то либо её производная в ней равняется нулю, либо производная в ней не существует.
Пусть точка $x'$ будет критической для $y=f(x)$ и принадлежит интервалу $(a,b)$, причем на каждом интервале $\left(a,x'{\rm \ }\right)\ и\ (x'{\rm \ },b)$ производная $f'(x)$ существует и сохраняет один и тот же знак. В этом случае:
- Если в $(a,x'{\rm \ })$ $f'\left(x\right) >0$, а в $(x'{\rm \ },b)$ $f'\left(x\right)
- Если в $(a,x'{\rm \ })$ $f'\left(x\right)0$, то $x'$ --будет точкой минимума для этой функции.
- Если и в $(a,x'{\rm \ })$, и в $(x'{\rm \ },b)$ производная $имеет\ один\ и\ тот\ же\ постоянный\ знак$, то $x'$ не будет точкой экстремума для этой функции.
На рисунке 1 мы можем наглядно увидеть смысл теоремы 2.
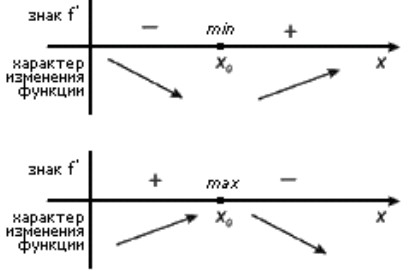
Рисунок 1.
Примеры точек экстремумов вы можете видеть на рисунке 2.
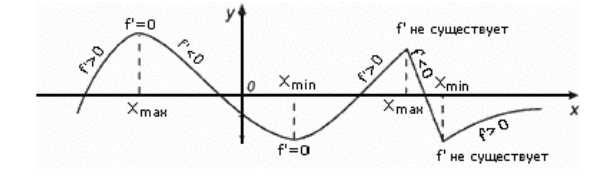
Рисунок 2.
Правило исследования на экстремум
- Найти $D(f)$;
- Найти $f'(x)$;
- Найти точки, где $f'\left(x\right)=0$;
- Найти точки, где $f'(x)$ не будет существовать;
- Отметить на координатной прямой $D(f)$ и все найденные в 3 и 4 пункте точки;
- Определить знак $f'(x)$ на полученных промежутках;
- Используя теорему 2, сделать заключение по поводу всех найденных точек.
Возрастание и убывание функции
Функция $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1
Функция $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть убывающей, если для любых точек $x_1,x_2\in X$ при $x_1f(x_2)$.
Чаще всего функции исследуют на возрастание и убывание с помощью средств математического анализа, а именно производной.
Приведем схему для такого исследования.
- \item Найти $D(f)$;
- Найти $f'(x)$;
- Найти точки, где $f'\left(x\right)=0$;
- Найти точки, где $f'(x)$ не будет существовать;
- Отметить на координатной прямой $D(f)$ и все найденные выше точки;
- Определить знак $f'(x)$ на всех получившихся промежутках;
- Сделать вывод: там, где $f'\left(x\right)0$ функция будет возрастать.
Пример задачи
Исследовать функцию на монотонность. $f(x)={4x}^3-30x^2+72x+13$
- $D\left(f\right)=R$;
- $f'\left(x\right)=12x^2-60x+72$;
-
$f'\left(x\right)=0$;
\[12x^2-60x+72=0\] \[x^2-5x+6=0\] \[x=3,\ x=2\] -
$f'(x)$ существует во всей $D(f)$;
-

Рисунок 3. - \[f'\left(x\right) >0,\ при\ \left(-\infty ,2\right)\ (3,+\infty )\] \[f'\left(x\right)
-
Изображая все на одном рисунке, получим:
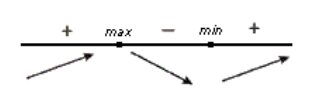
Рисунок 4.
Вывод:
Функция будет возрастать в промежутках $\left(-\infty ,2\right)\ (3,+\infty )$, функция будет убывать в промежутках $\left(2,3\right)$.












