Квадратичная функция
Часто квадратичную функцию применяют при решении различных задач, которые сводятся к нахождению тех или иных наибольших или наименьших значений. Но перед рассмотрением таких задач стоит напомнить, какая функция является квадратичной и как найти наибольшее/наименьшее значение.
Функция, имеющая вид $y=ax^2+bx+c$, где $a$ не равняется нулю, называется квадратичной функцией.
График такой функции принято называть параболой. Отметим, что если $a >0$ то ее ветви будут направлены вверх и ее вершина будет принимать минимальное значение, а если $a
Наибольшее и наименьшее значение
Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наибольшее значение в точке $x'\in X$, если выполняется
\[f\left(x\right)\le f(x')\]Функция $y=f(x)$, которая имеет областью определения множество $X$, имеет наименьшее значение в точке $x'\in X$, если выполняется
\[f\left(x\right)\ge f(x')\]Чтобы найти наименьшее и наибольшее значение заданной функции на каком либо отрезке необходимо произвести следующие действия:
- Найти $f'(x)$;
- Найти точки, в которых $f'\left(x\right)=0$;
- Найти точки, в которых $f'(x)$ не будет существовать;
- Выкинуть из точек, найденных в пунктах 2 и 3 те, которые не лежат в отрезке $[a,b]$;
- Вычислить значения в оставшихся точках и на концах $[a,b]$;
- Выбрать из этих значений наибольшее и наименьшее.
Приведем пример на нахождение наибольшего и наименьшего значения функции.
Найти наибольшее и наименьшее значения на [0,6]:$f\left(x\right)=x^3-3x^2-45x+225$
Решение.
- $f'\left(x\right)=3x^2-6x-45$;
-
$f'\left(x\right)=0$;
\[3x^2-6x-45=0\] \[x^2-2x-15=0\] \[x=5,\ x=-3\] -
$f'(x)$ существует на всей $D(f)$;
- $5\in \left[0,6\right]$;
-
Значения:
\[f\left(0\right)=225\] \[f\left(5\right)=50\] \[f\left(6\right)=63\] -
Наибольшее значение равняется $225$, наименьшее равняется $50.$
Ответ: $max=225,\ min=50$.
Рассмотрим далее задачи на использование наибольшего и наименьшего значений квадратичной функции.
Примеры задач
По перекрестным дорогам движутся два автомобиля в сторону перекрестка. Каждому автомобилю до перекрестка ехать по $50$ км. Автомобили движутся со скоростями $30$ и $40$ км/ч, соответственно. Найти, когда автомобили будут друг от друга на наименьшем расстоянии и на каком.
Решение.
Изобразим ситуацию на рисунке (рис. 1).
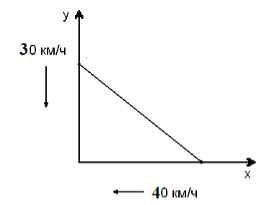
Рисунок 1.
Пусть наименьшее расстояние между автомобилями будет в момент времени $t$.
В это время одному автомобилю до перекрестка остается ехать
\[50-30t\ км\]А второму
\[50-40t\ км\]Расстояние между ними, по теореме Пифагора, будет равняться
\[S\left(t\right)={(50-30t)}^2+{(50-40t)}^2=2500-3000t+{900t}^2+2500-4000t+{1600t}^2={2500t}^2-7000t+5000\]Найдем наименьшее значение такой функции
\[t=-\frac{b}{2a}=-\frac{-7000}{5000}=\frac{7}{5}=1,4\] \[S\left(t\right)=2500\cdot \frac{49}{25}-7000\cdot \frac{7}{5}+5000=4900-9800+5000=100\]Ответ: $1$ ч $24$ мин, $100$ км.
Найти на графике функции $y=x+2$ точку, которая дает наименьшую сумму квадратов расстояний от него до точки $(8,0)$ и $(1,0)$.
Решение.
Рассмотрим рисунок:
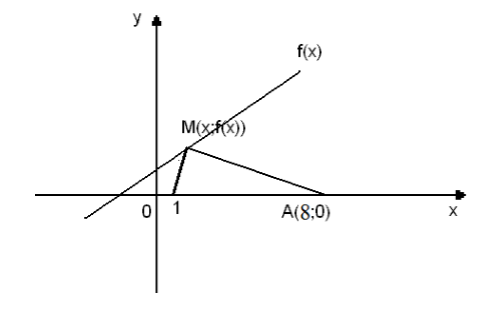
Рисунок 2.
Обозначим абсциссу искомой точки через $x$. Точка искомая точка имеет вид $(x,x+1)$.
Найдем расстояние до точки $(8,0)$: $\sqrt{{(8-x)}^2+{(x+1)}^2}$
Найдем расстояние до точки $(1,0)$: $\sqrt{{(1-x)}^2+{(x+1)}^2}$
Получаем, сумма равна
\[S\left(x\right)={(8-x)}^2+{(x+1)}^2+{(1-x)}^2+{(x+1)}^2=64-16x+x^2+1+2x+x^2+1-2x+x^2+1+2x+x^2=4x^2+18x+67\]Наименьшее значение
\[x=-\frac{18}{8}=-\frac{9}{4}=-2,25\] \[y=\frac{81}{4}-\frac{162}{4}+\frac{268}{4}=\frac{187}{4}=46,75\]Ответ: $(-2,25;46,75)$











