Функция $f(x)=x^2$
Определим для начала квадратичную функцию.
Функция, имеющая вид $y=ax^2+bx+c$, где $a$ не равняется нулю, называется квадратичной функцией.
Если теперь в определении 1 принять, что $a=1,\ \ b,c=0$ то мы и получим функцию вида $y=x^2$, которая интересует нас в этом пункте.
Исследуем и построим её график.
- $D\left(f\right)=R$.
- По определению квадрата любого действительного числа, получим $E\left(f\right)=[0,\infty )$
- $f\left(-x\right)={(-x)}^2=x^2=f(x)$. Следовательно, эта функция будет четной.
- При $x=0,\ y=0$. Значит начало координат принадлежит данной функции. Это единственная точка пересечения с координатными осями.
-
$f'\left(x\right)={\left(x^2\right)}'=2x$
\[2x=0,\] \[x=0\]Функция будет возрастать на промежутке $x\in (0,+\infty )$
Функция будет убывать на промежутке $x\in (-\infty ,0)$
-
$f^{''}\left(x\right)={\left(2x\right)}^{''}=2>0$.
Функция будет вогнутой на всей $D(f)$.
-
Значения на концах области определения.
\[{\mathop{\lim }_{x\to -\infty } x^2\ }=+\infty \] \[{\mathop{\lim }_{x\to +\infty } x^2\ }=+\infty \] -
График данной функции называется параболой. Он изображен на рисунке 1.
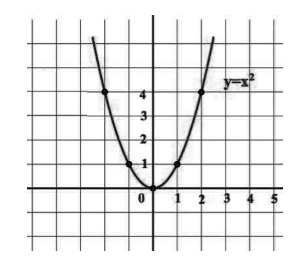
Рисунок 1.
Функция $f(x)=\frac{k}{x}$
По-другому функцию такого вида еще можно назвать функцией обратной пропорциональности. Введем ее определение.
Функция, имеющая вид $y=\frac{k}{x}$, где $k$ не равняется нулю и область определения исключает ноль, называется функцией обратной пропорциональности.
Исследуем и построим её график для двух различных случаев.
-
$k >0$
- $D\left(f\right)=R$.
- Очевидно, что эта функция никогда не будет равняться нулю, следовательно, $\ E\left(f\right)=\left(-\infty ,0\right)\cup (0,\infty )$
- $f\left(-x\right)=\frac{k}{-x}=-\frac{k}{x}=-f(x)$. Следовательно, эта функция будет нечетной.
- Данная функция не имеет ни одной точки пересечения с координатными осями.
-
$f'\left(x\right)={\left(\frac{k}{x}\right)}'=-\frac{k}{x^2}$
\[-\frac{k}{x^2}=0-нет\ корней\]Функция убывает на всем промежутке области определения
-
$f^{''}\left(x\right)={\left(-\frac{k}{x^2}\right)}^{''}=\frac{k}{x^3}$.
Функция будет вогнутой на промежутке $x\in (0,\infty )$.
Функция будет выпуклой на промежутке $x\in (-\infty ,0)$.
-
Значения на концах области определения: при стремлении к отрицательной и положительной бесконечности функция будет стремиться к нулю.
При приближении к нулю слева функция стремится к отрицательной бесконечности, а при приближении к нулю справа к положительной бесконечности.
-
График данной функции называется гиперболой. Она изображена на рисунке 2.
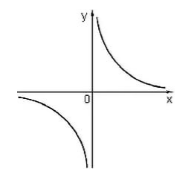
Рисунок 2.
-
$k
- $D\left(f\right)=R$.
- Очевидно, что эта функция никогда не будет равняться нулю, следовательно, $\ E\left(f\right)=\left(-\infty ,0\right)\cup (0,\infty )$
- $f\left(-x\right)=\frac{k}{-x}=-\frac{k}{x}=-f(x)$. Следовательно, данная функция будет нечетной.
- Данная функция не имеет ни одной точки пересечения с координатными осями.
-
$f'\left(x\right)={\left(\frac{k}{x}\right)}'=-\frac{k}{x^2}$
\[-\frac{k}{x^2}=0-нет\ корней\]Функция возрастает на всем промежутке области определения
-
$f^{''}\left(x\right)={\left(-\frac{k}{x^2}\right)}^{''}=\frac{k}{x^3}$.
Функция будет выпуклой на промежутке $x\in (0,\infty )$.
Функция будет вогнутой на промежутке $x\in (-\infty ,0)$.
-
Значения на концах области определения: при стремлении к отрицательной и положительной бесконечности функция будет стремиться к нулю.
При приближении к нулю справа функция стремится к отрицательной бесконечности, а при приближении к нулю слева к положительной бесконечности.
-
Графиком данной функции называется гиперболой. Она изображена на рисунке 3.
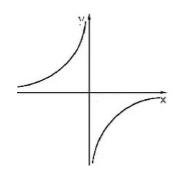
Рисунок 3.
Функция $f(x)=\frac{1}{x}$
Изобразить график функции $y=\frac{1}{x}$
Найдем ряд точек, принадлежащих данной функции.

Рисунок 4.
График имеет вид
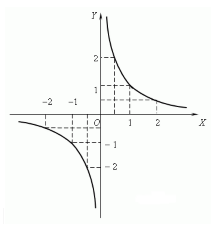
Рисунок 5.
Отметим, что она обладает свойствами, найденными в пункте 1 для гипербол. Переписать эти свойства для данного графика предоставляем читателю самостоятельно.













