Общие свойства функций и построение графиков

Источник статьи

Автор24 — учеба по твоим правилам

График функции и его построение

Определение 1

Графиком функции $f(x)$ будет называться множество точек координатной плоскости, которые имеют вид $(x,\ f\left(x\right))$ .

Схема для построения графиков функций:

Найти $D(f)$ и $E(f)$ .
Исследовать на свойство четности и нечетности, а также на свойство периодичности.
Найти пересечение с координатными осями и промежутки, на которых $f\left(x\right) >0$ и $f\left(x\right)
Найти промежутки где функция возрастает и убывает, найти экстремумы.
Найти интервалы выпуклости $и$ вогнутости функции.
Вычислить пределы на границах $D(f)$ .
Найти дополнительные точках при необходимости.
Изобразить график.

Четность и нечетность функции

Определение 2

Функцию $y=f(x)$ , которая имеет своей областью определения множество $X$ , будем называть четной, если для всех точек из множества $X$ будет выполняться

$f\left(x\right)=f(-x)$

График этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

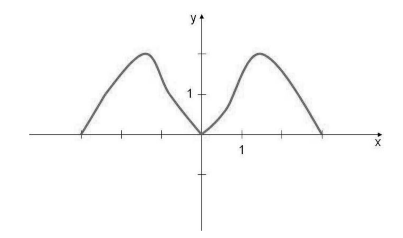
Рисунок 1.

Определение 3

Функцию $y=f(x)$ , которая имеет своей областью определения множество $X$ , будем называть нечетной, если для всех точек из множества $X$ будет выполняться

$f\left(-x\right)=-f(x)$

График этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).

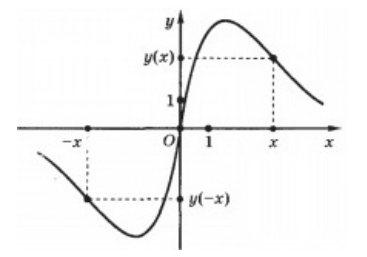
Рисунок 2.

Для исследования функции в её аналитической записи заменяют переменную $x$ на переменную $-x$ , производят, при необходимости элементарные преобразования, и проверяют условия определений 2 и 3.

Возрастание и убывание функции

Определение 4

Функция $y=f(x)$ , которая имеет своей областью определения множество $X$ , будем называть возрастающей, если подставив любые две точки получим, что $''$ будет верно $f(x')

Определение 5

Функция $y=f(x)$ , которая имеет своей областью определения множество $X$ , будем называть убывающей, если подставив любые две точки получим, что будет верно $f\left(x'\right) >f(x'')$ .

«Общие свойства функций и построение графиков» 👇

Помощь эксперта по теме работы

Найти эксперта

Решение задач от ИИ за 2 минуты

Решить задачу

Помощь с рефератом от нейросети

Написать ИИ

Чаще всего функции исследуют на возрастание и убывание с помощью средств математического анализа, а именно производной.

Приведем схему для такого исследования.

Найти $D(f)$ ;
Найти $f'(x)$ ;
точки, когда $f'\left(x\right)=0$ ;
точки, когда $f'(x)$ не будет существовать;
Отметить на координатной прямой $D(f)$ и все найденные выше точки;
знак $f'(x)$ на всех получившихся промежутках;
Сделать вывод: там, где $f'\left(x\right)0$ функция будет возрастать.

Выпуклость и вогнутость функции

Определение 6

Функция $y=f(x)$ , которая имеет своей областью определения множество $X$ будет называться выпуклой, если подставив любые две точки получим, что неравенство

$f\left(\frac{x'+x''}{2}\right)\le \frac{f(x')+f(x'')}{2}$

верно.

Определение 7

Функция $y=f(x)$ , которая имеет своей областью определения множество $X$ будет называться вогнутой, если подставив любые две точки получим, что неравенство

$f\left(\frac{x'+x''}{2}\right)\ge \frac{f(x')+f(x'')}{2}$

верно.

Схема исследования:

Найти

$D(f)$ ;
$f''(x)$ ;
точки, когда $f''\left(x\right)=0$ ;
точки, когда $f''(x)$ не будет существовать;
знак $f''(x)$ на каждом из найденных промежутков;
если $f''\left(x\right)0$ то вогнутой.

Пример исследования и построения функции

Пример 1

Исследовать данную функцию и построить график:

$f\left(x\right)=sinx-cosx$

$D\left(f\right)=R$
$\ E\left(f\right)=\left(-\infty ,0\right)\cup (0,+\infty ).$
$f\left(-x\right)=-cosx-sinx$
Следовательно, данная функция -- общего вида.
$sinx-cosx=0$ $x=\frac{\pi }{4}+\pi n,n\in Z$
Пересечение с осью $Ox$ : $\left(\frac{\pi }{4}+\pi n,0\right)$

Пересечение с осью $Oy$ : $\left(0,-1\right)$

На интервале $x\in \left(\frac{\pi }{4}+2\pi n,\frac{5\pi }{4}+2\pi n\right)$ функция будет принимать положительные значения, на интервале $x\in \left(-\frac{3\pi }{4}+2\pi n,\frac{\pi }{4}+2\pi n\right)$ функция будет принимать отрицательные значения.
$y'=sinx+cosx$ $sinx+cosx=0$ $x=-\frac{\pi }{4}+\pi n,n\in Z$
Функция возрастает на $\left(-\frac{\pi }{4}+2\pi n,\frac{3\pi }{4}+2\pi n\right)$ и убывает на $\left(\frac{3\pi }{4}+2\pi n,\frac{7\pi }{4}+2\pi n\right)$ .
$y^{''}=cosx-sinx$ $-sinx+cosx=0$ $x=\frac{\pi }{4}+\pi n,n\in Z$
На интервале $\left(\frac{\pi }{4}+2\pi n,\frac{5\pi }{4}+2\pi n\right)$ функция вогнута, на интервале $\left(-\frac{3\pi }{4}+2\pi n,\frac{\pi }{4}+2\pi n\right)$ функция выпукла.

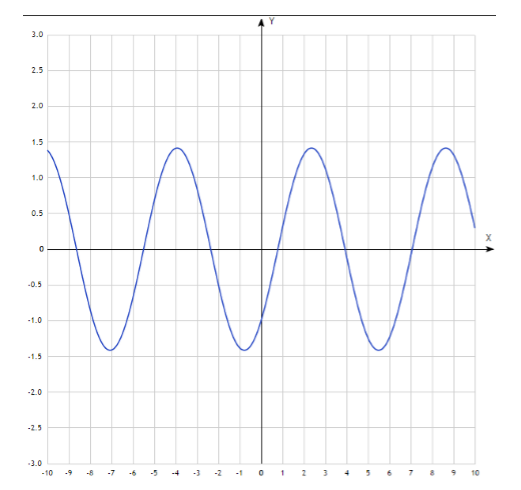
Рисунок 3.