Понятие линейного неравенства с двумя неизвестными
Неравенство $ax+by\cdot c$, где $\cdot$ один из следующих знаков $≥ ,>, ≤ ,линейным неравенством с двумя неизвестными.
$2x-y\ge 5$
Если при подстановке двух чисел в неравенство с двумя неизвестными оно становится верным, то эта пара чисел является решением этого неравенства.
Приведем теперь два свойства для понятия линейных неравенств с двумя неизвестными:
- Одно и тоже число можно прибавлять к обоим сторонам неравенства, чтобы оно оставалось неизменным.
- При умножении обоих частей неравенства на положительное число оно останется неизменным.
- При умножении на отрицательное число и изменении знака на противоположный оно останется неизменным
Неравенства
\[x-2y >2\] \[x-2y+1 >3\] \[-3\left(x-2y+1\right)равносильны.График линейного неравенства с двумя неизвестными
Множество точек координатной плоскости, которые являются решением какого-либо линейного неравенства с двумя неизвестными называется решением этого неравенства.
Построим решение линейного неравенства $2x-y\ge -3$
Выражаем $y$ через $x$:
\[-y\ge -3-2x\] \[y\le 2x+3\]Строим прямую $y=2x+3$
Так как неравенство имеет знак «меньше или равно», получим решение, изображенное на рисунке $1$ ( на рисунке оно изображено серым цветом). Заметим, что прямая также входит в решение, так как в неравенстве присутствует знак равенства.
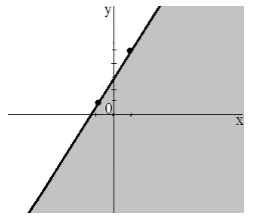
Рисунок 1.
Пример задач
Решить неравенство $x-y
Решение.
Выражаем $y$ через $x$:
\[-yx-1\]Изобразим график уравнения $y=x-1$
Так как последнее неравенство имеет знак «больше», получим решение, изображенное на рисунке $2$ ( на рисунке оно изображено серым цветом). Заметим, что прямая не входит в решение, так как в неравенстве не присутствует знак равенства.
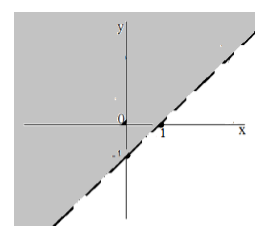
Рисунок 2.
Решить неравенство $x-2y\le 2$
Решение.
Выражаем $y$ через $x$:
\[-2y\le 2-x\] \[y\ge \frac{x}{2}-1\]Изобразим график уравнения $y=\frac{x}{2}-1$
Так как последнее неравенство имеет знак «больше или равно», получим решение, изображенное на рисунке $3$ (на рисунке оно изображено серым цветом). Заметим, что прямая входит в решение, так как в неравенстве присутствует знак равенства.
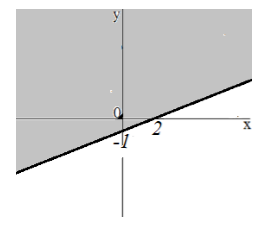
Рисунок 3.
Решить неравенство $x-y\ge 0$
Решение.
Выражаем $y$ через $x$:
\[-y\ge 2-x\] \[y\le x\]Изобразим график уравнения $y=x$
Так как последнее неравенство имеет знак «меньше или равно», получим решение, изображенное на рисунке $4$ (на рисунке оно изображено серым цветом). Заметим, что прямая входит в решение, так как в неравенстве присутствует знак равенства.
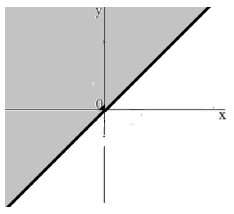
Рисунок 4.











