Четные функции
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться
\[f\left(x\right)=f(-x)\]Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
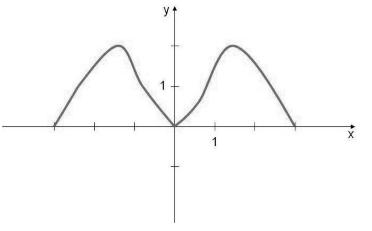
Рисунок 1.
Для исследования функции на четность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 1.
Нечетные функции
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться
\[f\left(-x\right)=-f(x)\]Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
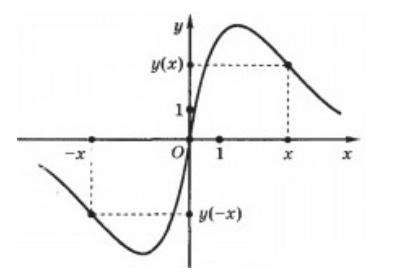
Рисунок 2.
Для исследования функции на нечетность необходимо в его аналитической записи заменить переменную $x$ на переменную $-x$, произвести, при необходимости элементарные преобразования, и проверить условие определения 2.
Функция общего вида
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть функцией общего вида, если она не будет ни четной, ни нечетной.
Для того чтобы понять, что данная функция является функцией общего вида, необходимо в его аналитической записи заменить переменную $x$ на переменную $--x$, произвести, при необходимости элементарные преобразования, и проверить невыполнение условий определений 1 и 2.
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
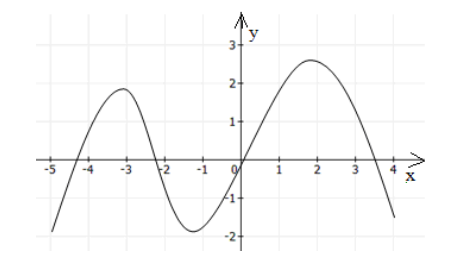
Рисунок 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
а) $f(x)=x^2+3$
б) $f(x)=\frac{x^2+4}{x}$
в) $f\left(x\right)=sinx+cosx$
Решение.
а) $f(x)=x^2+3$
$f\left(-x\right)={(-x)}^2+3=x^2+3=f(x)$\textit{ }следовательно, $f(x)$ -- четная функция.
Изобразим её на графике:
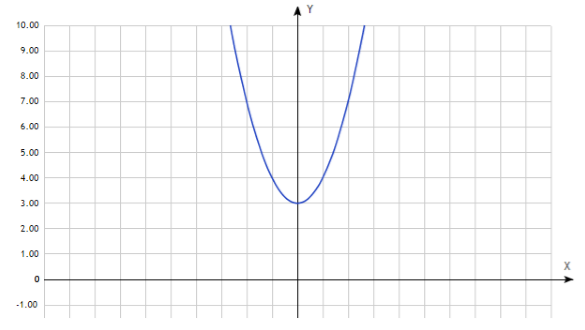
Рисунок 4.
б) $f(x)=\frac{x^2+4}{x}$
$f\left(-x\right)=\frac{{\left(-x\right)}^2+4}{-x}=-\frac{x^2+4}{x}$ следовательно, $f(x)$ -- нечетная функция.
Изобразим её на графике:
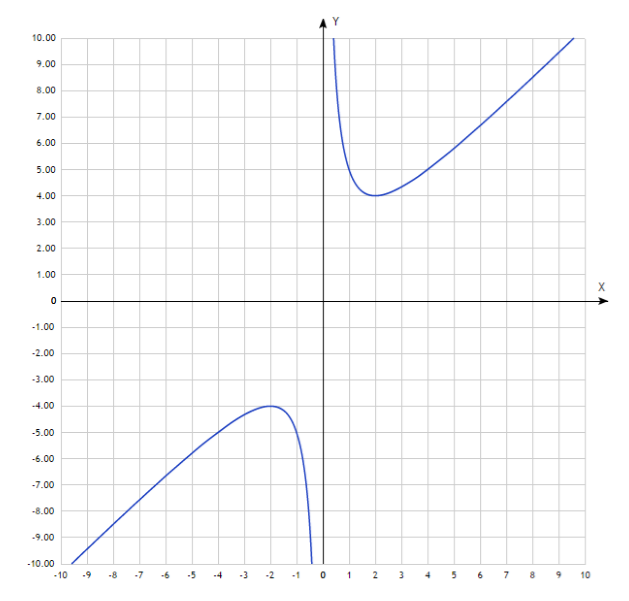
Рисунок 5.
в) $f\left(x\right)=sinx+cosx$
$f\left(-x\right)={\sin \left(-x\right)\ }+{\cos \left(-x\right)\ }=cosx-sinx$ следовательно, $f\left(x\right)$ -- функция общего вида.
Изобразим её на графике:
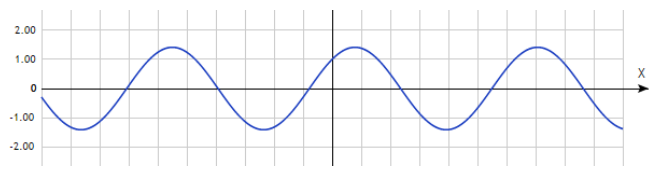
Рисунок 6.












