Основные понятия
Вспомним для начала определения четной, нечетной и периодической функции.
Четная функция -- функция, которая не меняет свое значение при изменении знака независимой переменной:
\[f\left(-x\right)=f(x)\]Функция, которая повторяет свои значения через некоторый регулярный интервал времени:
\[f\left(x\right)=f(x+T)\]T -- период функции.
Четность и нечетность тригонометрических функций
Рассмотрим следующий рисунок (рис. 1):
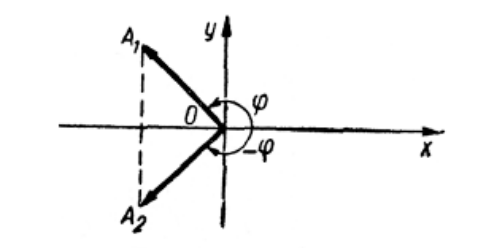
Рисунок 1.
Здесь $\overrightarrow{OA_1}=(x_1,y_1)$ и $\overrightarrow{OA_2}=(x_2,y_2)$ -- симметричные относительно оси $Ox$ векторы единичной длины.
Очевидно, что координаты этих векторов связаны следующими соотношениями:
Так как тригонометрические функции синуса и косинуса можно определять с помощью единичной тригонометрической окружности, то получаем, что функция синуса будет нечетной, а функция косинуса -- четной функцией, то есть:
Рассмотрим теперь функции тангенса и котангенса. Так как $tgx=\frac{sinx}{cosx}$, то
Так как $сtgx=\frac{cosx}{sinx}$, то
Периодичность тригонометрических функций
Рассмотрим следующий рисунок (рис. 2).
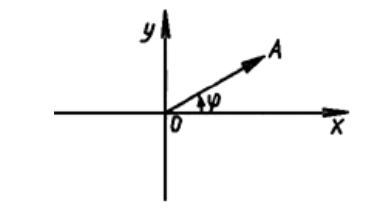
Рисунок 2.
Здесь $\overrightarrow{OA}=(x,y)$ -- вектор единичной длины.
Сделаем полный оборот вектором $\overrightarrow{OA}$. То есть повернем данный вектор на $2\pi $ радиан. После этого вектор полностью вернется в начальное положение.
Так как тригонометрические функции синуса и косинуса можно определять с помощью единичной тригонометрической окружности, то получаем, что
То есть функции синуса и косинуса являются периодическими функциями с наименьшим периодом $T=2\pi $.
Рассмотрим теперь функции тангенса и котангенса. Так как $tgx=\frac{sinx}{cosx}$, то
Так как $сtgx=\frac{cosx}{sinx}$, то
Примеры задач на использование четности, нечетности и периодичности тригонометрических функций
Доказать следующие утверждения:
а) $tg{385}^0=tg{25}^0$
б) ${cos \left(-13\pi \right)\ }=-1$
в) $sin{(-721}^0)=-sin1^0$
Решение.
а) $tg{385}^0=tg{25}^0$
Так как тангенс -- периодическая функция с минимальным периодом ${360}^0$, то получим
\[tg{385}^0=tg{(360}^0+{25}^0)=tg{25}^0\]б) ${cos \left(-13\pi \right)\ }=-1$
Так как косинус -- четная и периодическая функция с минимальным периодом $2\pi $, то получим
\[{cos \left(-13\pi \right)\ }={cos 13\pi \ }={cos \left(\pi +6\cdot 2\pi \right)=cos\pi \ }=-1\]в) $sin{(-721}^0)=-sin1^0$
Так как синус -- нечетная и периодическая функция с минимальным периодом ${360}^0$, то получим
\[sin{(-721}^0)=-sin{721}^0=-{sin \left({720}^0+1^0\right)\ }=-sin1^0\]











