Понятие движения
Разберем сначала такое понятие как движение.
Отображение плоскости называется движением плоскости, если при этом отображении сохраняются расстояния.
Существуют несколько теорем, связанных с этим понятием.
Треугольник, при движении, переходит в равный ему треугольник.
Любая фигура, при движении, переходит в равную ей фигуру.
Осевая и центральная симметрия являются примерами движения. Рассмотрим их более подробно.
Осевая симметрия
Точки $A$ и $A_1$ называются симметричными относительно прямой $a$, если эта прямая перпендикулярна к отрезку ${AA}_1$ и проходит через его центр (рис. 1).
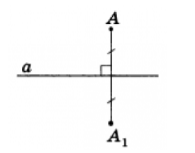
Рисунок 1.
Рассмотрим осевую симметрию на примере задачи.
Построить симметричный треугольник для данного треугольника относительно какой-либо его стороны.
Решение.
Пусть нам дан треугольник $ABC$. Будем строить его симметрию относительно стороны $BC$. Сторона $BC$ при осевой симметрии перейдет в саму себя (следует из определения). Точка $A$ перейдет в точку $A_1$ следующим образом: ${AA}_1\bot BC$, ${AH=HA}_1$. Треугольник $ABC$ перейдет в треугольник $A_1BC$ (Рис. 2).
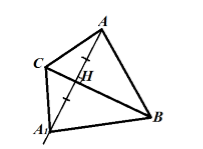
Рисунок 2.
Фигура называется симметричной относительно прямой $a$, если каждая симметричная точка этой фигуры содержится на этой же фигуре (рис. 3).
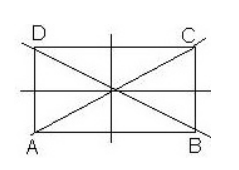
Рисунок 3.
На рисунке $3$ изображен прямоугольник. Он обладает осевой симметрией относительно каждого своего диаметра, а также относительно двух прямых, которые проходят через центры противоположных сторон данного прямоугольника.
Центральная симметрия
Точки $X$ и $X_1$ называются симметричными относительно точки $O$, если точка $O$ является центром отрезка ${XX}_1$ (рис. 4).
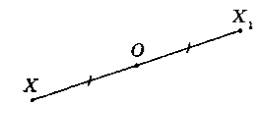
Рисунок 4.
Рассмотрим центральную симметрию на примере задачи.
Построить симметричный треугольник для данного треугольника какой-либо его вершины.
Решение.
Пусть нам дан треугольник $ABC$. Будем строить его симметрию относительно вершины $A$. Вершина $A$ при центральной симметрии перейдет в саму себя (следует из определения). Точка $B$ перейдет в точку $B_1$ следующим образом ${BA=AB}_1$, а точка $C$ перейдет в точку $C_1$ следующим образом: ${CA=AC}_1$. Треугольник $ABC$ перейдет в треугольник ${AB}_1C_1$ (Рис. 5).
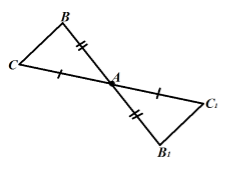
Рисунок 5.
Фигура является симметричной относительно точки $O$, если каждая симметричная точка этой фигуры содержится на этой же фигуре(рис. 6).
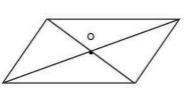
Рисунок 6.
На рисунке $6$ изображен параллелограмм. Он обладает центральной симметрией относительно точки пересечения его диагоналей.
Пример задачи.
Пусть нам дан отрезок $AB$. Построить его симметрию относительно прямой $l$, не пересекающий данный отрезок и относительно точки $C$, лежащей на прямой $l$.
Решение.
Изобразим схематически условие задачи.
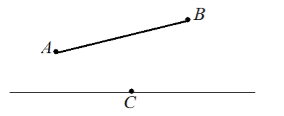
Рисунок 7.
Изобразим для начала осевую симметрию относительно прямой $l$. Так как осевая симметрия является движением, то по теореме $1$, отрезок $AB$ отобразится на равный ему отрезок $A'B'$. Для его построение сделаем следующее: проведем через точки $A\ и\ B$ прямые $m\ и\ n$, перпендикулярно прямой $l$. Пусть $m\cap l=X,\ n\cap l=Y$. Далее проведем отрезки $A'X=AX$ и $B'Y=BY$.
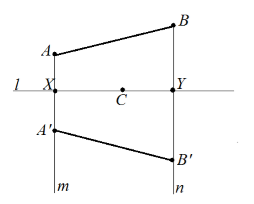
Рисунок 8.
Изобразим теперь центральную симметрию относительно точки $C$. Так как центральная симметрия является движением, то по теореме $1$, отрезок $AB$ отобразится на равный ему отрезок $A''B''$. Для его построения сделаем следующее: проведем прямые $AC\ и\ BC$. Далее проведем отрезки $A^{''}C=AC$ и $B^{''}C=BC$.
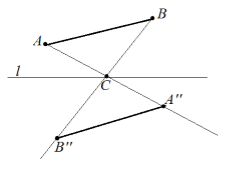
Рисунок 9.











