Рациональные числа
По ранее изученному материалу мы знаем, что рациональными числами называется множество чисел, содержащее в себе множество целых и дробных чисел и обозначается $Q.$
Любое рациональное число, как целое, так и дробное можно представить в виде дроби, где $a$- целое число, а $b$- натуральное и то, что любое рациональное число может быт представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби
Представление числа в виде конечной десятичной дроби
Попробуем воспользовавшись этими знаниями представить дробь, в виде десятичной дроби
Решение. Для того чтобы представить обычную дробь в виде десятичной, мы разделим числитель на знаменатель
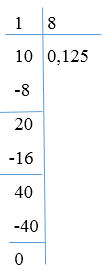
Рисунок 1.
Данную дробь мы представили в виде конечной десятичной дроби еще раз подтвердив то, что любое рациональное число можно представить в виде десятичной дроби, в данном случае конечной.
Представление числа в виде бесконечной десятичной периодической дроби
Представить дробь $в$иде десятичной.
Решение: Для того чтобы выполнить поставленную задачу, так же, как и в предыдущем задании, разделим числитель на знаменатель. Тогда, получим следующие вычисления
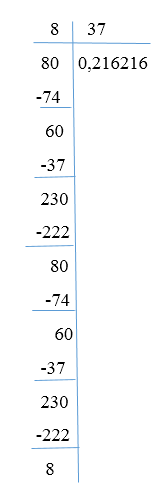
Рисунок 2.
Рассмотрим остатки, которые мы получала при делении. Первый из них равен $8$, второй-$6$, третий $23$.После этого четвертый и последующие равны вновь $8,6$ и $23$.Если мы будем продолжать деление, то очевидно следующие остатки будут вновь такими же и значит, сколько бы мы не продолжали деление в остатке не получится $0$, т.е. деление не остановится.
В таких случаях мы имеем дело с бесконечными десятичными дробями. записать это можно так:
\[\frac{8}{37}=0,216216\dots \dots \dots \]При подобной записи видно, что число 216 будет повторяться бесконечное количество раз, такие дроби называют периодическими. Повторяющиеся цифры называют периодом дроби. Очевидно, что в нашем случае период будет равен $216$. Записывают так:
$\frac{8}{37}=0,216216\dots \dots \dots =0, (216)$
Теперь мы убедились, что любое рациональное число может быть представлено в виде конечной десятичной дроби или бесконечной десятичной периодической дроби.
Проверим верно ли обратное. Попробуем представить бесконечную десятичную периодическую дробь в виде обыкновенной дроби.
Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь $1, (23)$
Решение. Запишем дробь раскрыв» период $1, (23) =1,232323\dots \dots.$
Теперь обратим внимание на то, что в период дроби входят сотые доли, значит для того, чтобы запятая сдвинулась на один период вправо необходимо умножить ее на $100$. Положим, что некоторое число
$a=1,232323\dots \dots$ тогда после умножения на $100$ получим
$100a=123,2323\dots \dots.$
Составим разность:

Рисунок 3.
Полученная дробь неправильная, преобразуем ее путем выделения целой части, $a=\frac{122}{99}=1\frac{23}{99}$. Другими словами, $1, (23) =1,232323\dots \dots .=1\frac{23}{99}$.
Аналогично можно доказать и правильность следующих равенств
$0,(3)= \frac{1}{3}; \ 2, (36)= 2\frac{4}{11}; \ 0,0(945) = \frac{7}{74}$
Проверим первое : $0, (3) =0,333\dots \dots \dots \dots.$
обратим внимание на то, что в период дроби входят десятые доли, значит для того, чтобы запятая сдвинулась на один период вправо необходимо умножить ее на $10$. Положим, что некоторое число
$b=0,333\dots \dots$, тогда после умножения на $10$ получим
$10b=3,33\dots \dots.$
Составим разность:
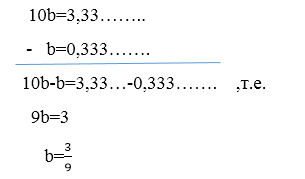
Рисунок 4.
Дробь сократима, воспользовавшись основным свойством дроби разделим числитель и знаменатель на $3$
\[\frac{3}{9}=\frac{1}{3}\]Тогда мы доказали, что $0, (3) = \frac{1}{3}$

















