Понятие делимости
Понятие делимости является одним из основных в арифметике и теории чисел.
Число $a$ делится на $b$, если существует такое число $q$, что выполняется:
$a = b\cdot q$,
где $a, b, q$ – целые числа, $b≠0$.
$b$ называют делителем числа $a$, a – кратным числа $b$, $q$ – частным.
Также принято говорить «$b$ делит $a$» или «$a$ делится на $b$ нацело».
Не для каждой пары целых чисел $a$ и $b$ существует такое целое число $q$, когда выполняется равенство $a=b\cdot q$. Тогда говорят «$a$ не делится на $b$» (при этом имеют в виду, что $a$ не делится на $b$ нацело). В таких случаях можно прибегнуть к делению целых чисел с остатком.
Рассмотрим понятие делимости на примерах.
Целое число $39$ делится на целое число $13$, т.к. $39=13\cdot 3$. Можно также сказать «число $13$ делит $39$».
В данном случае целое число $39$ является кратным числа $13$, а число $13$ – делителем числа $39$.
Целое число $27$ не делится на число $4$, т.к. не существует такого целого числа $q$, для которого выполняется равенство $27=4\cdot q.$
Т.е. в данном случае число $27$ не является кратным числа $4$, а число $4$ – делителем числа $27$.
Для удобства описания делимости принято использовать некоторые обозначения:
- $«⋮»$ – $3$ точки, расположенные по вертикали – обозначает тот факт, что $a$ кратно $b$. Записывают $a⋮b$. Например, запись $51⋮3$ означает, что целое число $51$ делится на $3$.
- $«|»$, «\» – вертикальная черта или левый слэш – обозначает тот факт, что число $b$ делит число $a$. Записывают $b|a$ или $b$\$a$. Например, запись $3|51$ означает, что число $3$ делит $51$.
-
зачеркнутые $3$ точки, расположенные по вертикали
– обозначают тот факт, что $a$ не кратно $b$. Например,
Рисунок 1.
– «$38$ не делится на $5$, $38$ не является кратным числа $5$, $38$ не кратно $5$».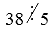
Рисунок 2. -
– зачеркнутая вертикальная черта – обозначают, что $b$ не делит $a$. Например,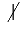
Рисунок 3.
– «$5$ не делит число $38$».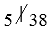
Рисунок 4.
Свойства делимости
-
Любое целое число делится само на себя, на противоположное себе, на $1$ и $–1$:
-
$a⋮a$ – свойство рефлексивности
-
$a⋮(-a)$
-
$a⋮1$
-
$a⋮(-1)$
-
-
Нуль делится на любое целое число:
- $0⋮a$
Частным случаем также является делимость нуля на нуль:
- $0⋮0$
Замечание 1Необходимо отметить, что другое целое число, не равное нулю, на нуль не делится:
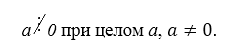
Рисунок 5. Если целое число $a$ делится на целое число $b$ и выполняется условие $\left|a\right|
-
Если целое число $a\ne 0$ и $a\vdots b$, то $\left|a\right|\ge \left|b\right|$. Данное свойство делимости вытекает из предыдущего.
-
Единица имеет только два делителя -- целые числа $(1)$ и $(-1)$.
-
Чтобы целые числа $a\vdots b$ необходимо и достаточно, чтобы $\left|a\right|\vdots \left|b\right|$.
Следствие 1.
Если $a\vdots b$, то $a\vdots \left(-b\right);$
$a$, $b$-- целые числа.
Следствие 2.
Если $a\vdots b$, то $\left(-a\right)\vdots b;$
$a$, $b$-- целые числа.
-
Свойство транзитивности:
Если $a\vdots m$ и $m\vdots b$, то $a\vdots b$;
$a, b, m$-- целые числа.
-
Свойство антисимметричности:
Если $a\vdots b$ и $b\vdots a$, то $a=b$ или $a=-b$;
$a, b$-- целые числа.
-
Для любого целого числа $b\ne 0$ найдется такое целое число $a\ne b$, которое делится на $b$.
-
Если $a\vdots c$ и $b\vdots c$, то $\left(a+b\right)\vdots c$,
$a, b, c$ -- целые числа.
-
Если $a\vdots b$, то $a\cdot k\vdots b$,
$a, b, k$-- целые числа.
Делители
Целое число $b$ называют делителем целого числа $a$, если число $a$ делится на $b$ без остатка.
Целое число $b$ называют делителем целого числа $a$, если существует такое целое число $q$, что выполняется равенство $a=b\cdot q$.
Число $-3$ является делителем числа $27$, т.к. выполняется равенство $27=\left(-3\right)\cdot \left(-9\right)$. Целое число $27$ имеет еще несколько делителей: $-27$, $-9$, $-3$, $-1$, $1$, $3$, $9$, $27$. Число, например, $4$ не является делителем числа $27$, т.к. не существует такого числа $q$, чтобы выполнялось равенство $27=4\cdot q$.
Кратные
Целое число $a$ называется кратным целого числа $b$, если оно делится на $b$ без остатка.
Целое число $a$ называется кратным целого числа $b$, если существует такое целое число $q$, что выполняется равенство $a=b\cdot q$.
Число $20$ является кратным числа $-4$, т.к. выполняется равенство $20=\left(-4\right)\cdot \left(-5\right)$. Целое число $-4$ имеет другие кратные ему целые числа: $0, 4, -4, 8, -8, 12, -12$ и т.д. Число $6$ не является кратным числа $-4$, т.к. $6$ не делится на $-4$ без остатка, т.е. не существует такое целое число $q$, что выполняется равенство $6=(-4)\cdot q$.













