Понятие компланарности векторов
Для начала рассмотрим, какие вектора называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Рассмотри, компланарны ли векторы a, b и c на следующем примере. Пусть нам даны три вектора →a1, →a2 и →a3. Тогда
Пары векторов →a1, и →a2, →a2 и →a3 и →a1 и →a3 компланарны между собой.
Если два из этих векторов, к примеру →a1, и →a2, коллинеарны, то векторы →a1, →a2 и →a3 компланарны.
Если →a1, →a2 и →a3 лежат в одной плоскости, то они компланарны.
Для дальнейшего рассмотрения напомним следующую теорему.
Произвольный вектор →p можно разложить по двум неколлинеарным векторам →a1, и →a2 с единственными коэффициентами разложения, то есть
→p=α1→a1+α2→a2Теоремы, связанные с условием компланарности трех векторов
Пусть нам даны три вектора →a, →b и →c.
Если один из трех данных векторов можно разложить по двум другим векторам, то есть
→c=α→a+β →bгде α и β - действительные числа, то векторы →a, →b и →c являются компланарными векторами.
Доказательство.
Здесь возможны два случая.
Векторы →a и →b - коллинеарные векторы. Но это условие неприменимо, если одна из координат вектора приравнивается нулю.
В этом случае компланарность векторов →a, →b и →c очевидна.
Векторы →a и →b не являются коллинеарными.
Так как вектор →c имеет свое разложение по двум неколлинеарным векторам →a и →b. Значит эти векторы попадают под условие теоремы 1, и, следовательно, векторы →a, →b и →c лежат в одной плоскости, то есть являются компланарными.
Теорема доказана.
Если три вектора →a, →b и →c являются компланарными, а векторы →a и →b не являются коллинеарными, то вектор →c можно единственным образом разложить по векторам →a и →b, то есть
→c=α→a+β →bДоказательство.
Так как векторы →a, →b и →c компланарны, то значит в произвольной плоскости γ, которой параллельны эти векторы, можно построить векторы →a′=→a, →b′=→b и →c′=→c. Так как векторы →a и →b не коллинеарны, то и векторы →a′ и →b′ не коллинеарны, тогда, по теореме 1, вектор →c′ можно разложить по векторам →a′ и →b′ следующим образом
→c′=α→a′+β →b′Причем это разложение единственно.
Следовательно
→c=α→a+β →bКоторое также единственно.
Теорема доказана.
Признак и критерий компланарности векторов
Пусть нам даны векторы →a=(a1,a2,a3), →b=(b1,b2,b3) и →c=(c1,c2,c3). Три вектора будут компланарны, если выполняется следующее условие:
компланарности векторов. Автор24 — интернет-биржа студенческих работ" />
Рисунок 1. Условие компланарности векторов. Автор24 — интернет-биржа студенческих работ
Пример задачи
Пусть нам дан куб ABCDA1B1C1D1. Разложите вектор →A1C1 по векторам →AB и →BC.
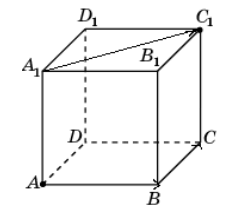
Рисунок 2. Разложение по векторам. Автор24 — интернет-биржа студенческих работ
Решение.
Так как плоскости (ABC) и (A1B1C1) параллельны, и векторы →A1C1, →AB и →BC параллельны, следовательно, по определению являются компланарными. Тогда, по теореме 1, вектор →A1C1 можно разложить по векторам →AB и →BC единственным образом.
Используя свойства сложения двух векторов, получим
→A1C1=→A1B1+→B1C1Так как
→A1B1=→AB, →B1C1=→BCСледовательно
→A1C1=→AB+→BCОтвет: →AB+→BC.
Пусть нам дан параллелепипед. Найти тройки компланарных векторов, изображенных в параллелепипеде на рисунке ниже.
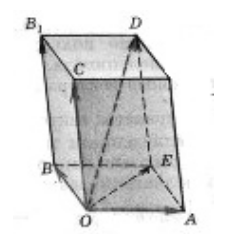
Рисунок 3. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Так как векторы →OA, →OB и →OE лежат в плоскости (BOA) то эти векторы являются компланарными.
Так как векторы →OC, →OB и →BB1 лежат в плоскости (BOC) то эти векторы являются компланарными.
Так как векторы →OC, →OD и →OE лежат в плоскости (COE) то эти векторы являются компланарными.
Доказать, что векторы с координатами (1, 13, 2), (3, −5, 2)и (5,−1,4) компланарны.
Решение.
Применим признак компланарности трех векторов.
Найдем определитель
Рисунок 4. Нахождение определителя. Автор24 — интернет-биржа студенческих работ
Следовательно, это векторы компланарны, ч. т. д.
