
Краткие исторические сведения
Первоначально Р.Тафт предложил соотношение
где величина ${\sigma }^*$ определялась для группы заместителей $R$ из выражения
Выяснив, что ${\sigma }^*$-константы групп $XCH_2$ коррелируют с константами кислотности $XCH_2COOH$, Тафт предложил определять величины ${\sigma }_I$ для групп $X$ как ${\sigma }_I=0,45{\sigma }^*.$
Коэффициент $0,45$ брался из расчета сделать ${\sigma }_I$ --константу равной $lg\frac{K}{K_0}$ для ионизации кислот Робертса и Мореленда в воде.
Так как большую часть констант ${\sigma }_I$ получили из констант ионизации, то предпочтительнее считалось применять уравнение ${\sigma }_I=0,2621lg\frac{K}{K_0}$.
Уравнение Трафта для индукционного влияния заместителей
Р.Тафт описал ряд уравнений для количественного анализа влияния ближайших заместителей на реакционную способность соединения по данной функциональной группе. В настоящее время эти уравнения помогают определить механизм протекания реакции.
В своих исследованиях Тафт сравнил переходные состояния для кислотного и основного гидролиза сложных эфиров алифатических соединений. Он сделал следующие заключения:
- Пространственные взаимодействия и в кислотном и в основном гидролизе одинаковы, так как переходные состояния отличаются только числом протонов.
- В чисто алифатических соединениях заместители не будут проявлять мезомерные эффекты.
- Различное влияние заместителей на скорость гидролиза определено полярным эффектом, который оказывает различное влияние на противоположно заряженные переходные состояния.
Тафт предположил, что индукционное влияние, независимо от наличия или отсутствия резонансных и пространственных эффектов, можно описать выражением
где ${\rho }_I$ зависит только от реакции, а ${\sigma }_I$ зависит только от заместителя.
Для заместителя Х величина ${\sigma }_I$ определяется уравнением
где $K_0$- константа кислотности уксусной кислоты $CH_3COOH$;
$K$- константа кислотности замещенной кислоты $XCH_2COOH$ в водном растворе при $25^\circ C$.
Замена атома водорода в уксусной кислоте заместителем $X$ не может сопровождаться резонансными или стерическими влияниями.
Наибольшее значение имеет реакция ионизации $4-X$-бицикло[2,2,2]октанкарбоновых кислот и гидролиз их этиловых эфиров. В этих реакциях прослеживается хорошая линейная зависимость (Рис. 1)
![Корреляция констант ионизации $4$-замещенных бицикло[2,2,2]октанкарбоновых кислот с индукционными константами ${\sigma }_I$](/assets/files/articles/him389.png)
Рисунок 1. Корреляция констант ионизации $4$-замещенных бицикло[2,2,2]октанкарбоновых кислот с индукционными константами ${\sigma }_I$
В реакциях кислотного и основного гидролиза эфиров пространственные эффекты одинаковы. Если $k$ -- удельная скорость гидролиза $RCOOR`$, $k_0$ -- удельная скорость гидролиза $CH_3COOR`$, индекс $A$ относится к реакции в кислой среде, а $B$ -- в щелочной, то величина $A$ не зависит от пространственных эффектов.
Тафт усреднил величины $A$ для многих групп $R`$ в разных растворителях. Он показал линейную зависимость $lg\frac{K}{K_0}$ для ионизации $XCH_2COOH$ от $A$ для гидролиза $XCH_2COOR`$ с наклоном $0,236$ и стандартным отклонением $0,35$.
Корреляция реакционной способности алифатических и ароматических соединений
Для ионизации бензойных кислот между величинами $lg\frac{K}{K_0}$ и константами ${\sigma }_I$ не отмечается какой--либо зависимости. Разброс точек для заместителей достаточно велик (Рис. 2).
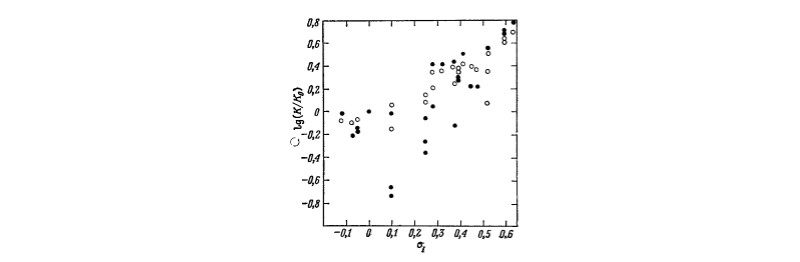
Есть данные, что константы ${\sigma }_I$, полученные из реакционной способности алифатических соединений, могут быть использованы для корреляции со свойствами производных бензолов.
Химический сдвиг фтора в м-производных фторбензола находится в линейной зависимости от ${\sigma }_I$. Этот сдвиг является чувствительным критерием электронной плотности вблизи атома фтора. Однако он показывает только те изменения плотности, которые связаны с индукционным эффектом.
Влияние $п$- и м-заместителей на реакционную способность включают дополнительные факторы.
Для одного и того же заместителя в $п$- и м-положениях в отсутствие прямого резонанса выражение
не зависит от реакции в пределах точности уравнения Гаммета.
Если принять, что оснований для абсолютной шкалы ${\sigma }_I$ или ${\sigma }^0_R$ нет, можно принять
тогда
Отсюда
Заместители находятся в порядке увеличения $\frac{{\sigma }^n}{{\sigma }_I}$ : $OCH_3$, $F$, $Cl$, $Br$, $I$, $NO_2$, $COOCH_3$, $CN$, $COCH_3$. График $\frac{{\sigma }^n}{{\sigma }_I}-\frac{{\sigma }^м}{{\sigma }_I}$ линейный (Рис. 3). Для $n$-заместителей в качестве ${\sigma }^n$ использовались ${\sigma }^0$-константы Тафта. $K_I=1$, $K_R$ находится в интервале от $2$ до $3$.
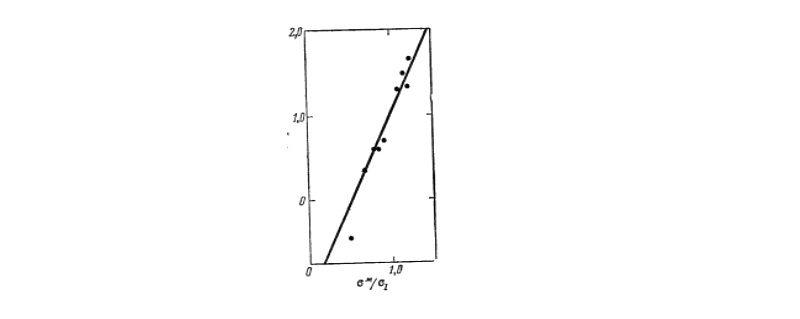
Рисунок 3. Зависимость $\frac{{\sigma }^n}{{\sigma }_I}и\frac{{\sigma }^м}{{\sigma }_I}$.











