Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные -- боковыми сторонами трапеции.
Средняя линия трапеции -- это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её векторным методом.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ -- средняя линия этой трапеции (рис. 1).
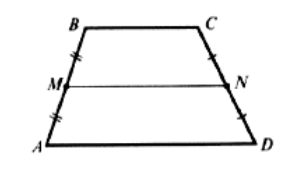
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.
Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ - середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
\[15\ см+17\ см=32\ см\]Следовательно, так как периметр равен $52\ см$, сумма оснований равна
\[52\ см-32\ см=20\ см\]Значит, по теореме 1, получаем
\[n=\frac{20\ см}{2}=10\ см\]Ответ: $10\ см$.
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
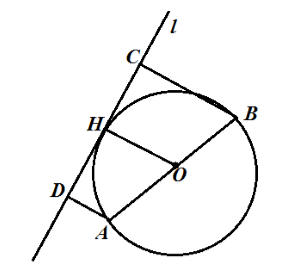
Рисунок 2.
Так как $AD$ и $BC$ - расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ -- радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ - трапеция, а $OH$ - ее средняя линия. По теореме 1, получаем
\[OH=\frac{AD+BC}{2}=\frac{9\ см+5\ см}{2}=7\ см.\]Значит
\[d=2OH=2\cdot 7\ см=14\ см.\]Ответ: $14$ см.
Доказать, что средняя линия трапеции проходит через середину произвольной диагонали данной трапеции.
Доказательство.
Пусть нам дана трапеция $ADCD$ со средней линией $MN$. Рассмотрим диагональ $AC$. Обозначим точкой $K$ - точку пересечения средней линии с этой диагональю (Рис. 3).
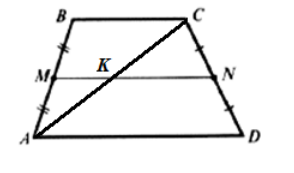
Рисунок 3.
Докажем, что $AK=KC$.
Так как $MN$ - средняя линия трапеции, то по теореме 1 $MN||BC$. Следовательно, $AM=NB$ и $MK||BC$. Тогда, по теореме о средней линии треугольника, получим что $MK$ - средняя линия треугольника $ABC$. Значит $AK=KC$.
ч. т. д.











