Решение простейших тригонометрических уравнений
Для начала вспомним формулы для решения простейших тригонометрических уравнений.
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Решение простейших тригонометрических неравенств.
Для решения простейших тригонометрических неравенств нам вначале необходимо решить соответствующее уравнение, а затем, используя тригонометрическую окружность, найти решение неравенства. Рассмотрим решения простейших тригонометрических неравенств на примерах.
$sinx\ge \frac{1}{2}$
Найдем решение тригонометрического неравенства $sinx=\frac{1}{2}$
\[x={(-1)}^narcsin\frac{1}{2}+\pi n,n\in Z\] \[x={(-1)}^n\frac{\pi }{6}+\pi n,n\in Z\]Отметим решение на тригонометрической окружности
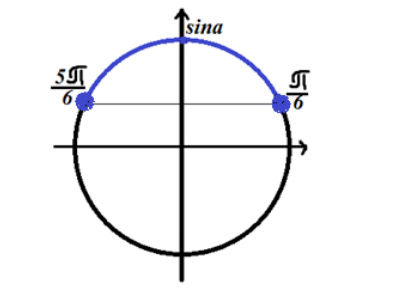
Рисунок 1. Решение неравенства $sinx\ge \frac{1}{2}$.
Так как неравенство имеет знак «больше или равно», то решение лежит на верхней дуге окружности (относительно решения уравнения).
Ответ: $\left[\frac{\pi }{6}+2\pi n,\frac{5\pi }{6}+2\pi n\right]$.
$cosx
Найдем решение тригонометрического неравенства $cosx=\frac{\sqrt{3}}{2}$
\[x=\pm arccos\frac{\sqrt{3}}{2}+2\pi n,n\in Z\] \[x=\pm \frac{\pi }{6}+2\pi n,n\in Z\]Отметим решение на тригонометрической окружности
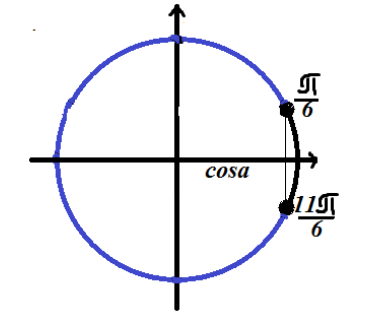
Так как неравенство имеет знак «меньше», то решение лежит на дуге окружности, расположенной слева (относительно решения уравнения).
Ответ: $\left(\frac{\pi }{6}+2\pi n,\frac{11\pi }{6}+2\pi n\right)$.
$tgx\le \frac{\sqrt{3}}{3}$
Найдем решение тригонометрического неравенства $tgx=\frac{\sqrt{3}}{3}$
\[x=arctg\frac{\sqrt{3}}{3}+\pi n,n\in Z\] \[x=\frac{\pi }{6}+\pi n,n\in Z\]Здесь также нам понадобится область определения. Как мы помним у функции тангенса $x\ne \frac{\pi }{2}+\pi n,n\in Z$
Отметим решение на тригонометрической окружности
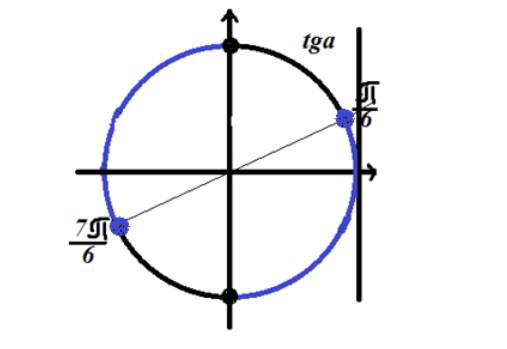
Рисунок 3. Решение неравенства $tgx\le \frac{\sqrt{3}}{3}$.
Так как неравенство имеет знак «меньше или равно», то решение лежит на дугах окружности, отмеченных синим на рисунке 3.
Ответ:$\ \left(-\frac{\pi }{2}+2\pi n\right.,\left.\frac{\pi }{6}+2\pi n\right]\cup \left(\frac{\pi }{2}+2\pi n,\right.\left.\frac{7\pi }{6}+2\pi n\right]$
$ctgx>\sqrt{3}$
Найдем решение тригонометрического неравенства $ctgx=\sqrt{3}$
\[x=arcctg\sqrt{3}+\pi n,n\in Z\] \[x=\frac{\pi }{6}+\pi n,n\in Z\]Здесь также нам понадобится область определения. Как мы помним у функции тангенса $x\ne \pi n,n\in Z$
Отметим решение на тригонометрической окружности
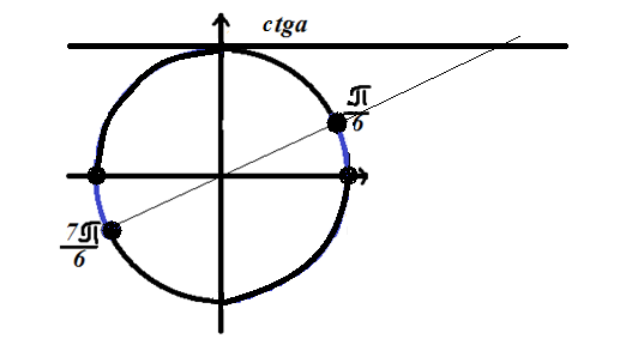
Рисунок 4. Решение неравенства $ctgx\le \sqrt{3}$.
Так как неравенство имеет знак «больше», то решение лежит на дугах окружности, отмеченных синим на рисунке 4.
Ответ:$\ \left(2\pi n,\frac{\pi }{6}+2\pi n\right)\cup \left(\pi +2\pi n,\frac{7\pi }{6}+2\pi n\right)$











