Понятие тригонометрических функций
Будем измерять величины углов в радианах. Поворот координатной плоскости вокруг начала координат на угол $\alpha $ радиан будем обозначать символом $R^{\alpha }$.
Через $P_{\alpha }$ будем обозначать точку единичной окружности $x^2+y^2=1$ которая получается из точки $P_0$ с координатами $(1,0)$ путем поворота плоскости вокруг начала координат на угол $\alpha $.
Рассмотрим в Декартовой системе координат окружность с радиусом $R>0$ и центром $(0,0)$ (рис. 1).
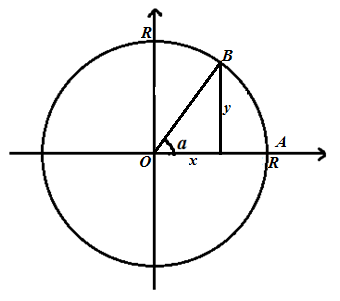
Рисунок 1. Окружность радиуса $R>0$.
$\left[OB\right]$ получается из $\left[OA\right]=R$ путем поворота на угол $\alpha $ радиан. Пусть $x$ и $y$ абсцисса и ордината точки $B$, соответственно, тогда
Так как в определениях синуса и косинуса их значения не зависят от радиуса окружности, то можно принять $R=1$. Поэтому, другим способом, тригонометрические значения определяются следующим образом:
Синусом острого угла называется ордината единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан.
Косинусом острого угла называется абсцисса единичной окружности, которая получается из точки $(1,\ 0)$ путем поворота на угол $\alpha $ радиан.
Тангенсом угла называется отношение значения синуса этого угла к значению косинуса этого угла.
Котангенсом угла называется отношение значения косинуса этого угла к значению синуса этого угла.
Функции $sinx$, $cosx$, $tgx$, $ctgx$ называются соответственно тригонометрическими функциями синуса, косинуса, тангенса и котангенса.
Свойства и график функции $f(x)=sinx$
- Область определения -- все числа.
- Область значения - отрезок $[-1,\ 1]$.
- Функция нечетна.
- Функция периодическая с минимальным периодом $2\pi $.
- При $x=0$, $y=0$. При $y=0$, $x=\pi n,n\in Z$.
- Функция выше оси $Ox$ при $x\in (2\pi n,\pi +2\pi n),n\in Z$.
- Функция ниже оси $Ox$ при $x\in (-\pi +2\pi n,2\pi n),n\in Z$.
- Функция $f\left(x\right)=sinx$ возрастает, при $x\in \left(-\frac{\pi }{2}+2\pi n,\frac{\pi }{2}+2\pi n\right)$.
Функция $f\left(x\right)=sinx$ убывает при $x\in \left(\frac{\pi }{2}+2\pi n,\frac{3\pi }{2}+2\pi n\right)$
Точки максимума $(\frac{\pi }{2}+2\pi n,1)$.
Точки минимума $(\frac{3\pi }{2}+2\pi n,-1)$.
- Функция непрерывна на всей области определения.
Графиком функции $y=sinx$ является синусоида (рис. 2).
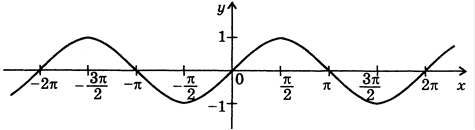
Рисунок 2. Синусоида.
Свойства и график функции $f(x)=cosx$
- Область определения -- все числа.
- Область значения - отрезок $[-1,\ 1]$.
- Функция четна.
- Функция периодическая с минимальным периодом $2\pi $.
- При $x=0$, $y=1$. При $y=0$, $x=\frac{\pi }{2}+\pi n,n\in Z$.
- Функция выше оси $Ox$ при $x\in \left(-\frac{\pi }{2}+2\pi n,\frac{\pi }{2}+2\pi n\right),n\in Z$.
- Функция ниже оси $Ox$ при $x\in \left(\frac{\pi }{2}+2\pi n,\frac{3\pi }{2}+2\pi n\right),n\in Z$.
- Функция $f\left(x\right)=cosx$ возрастает, при $x\in (-\pi +2\pi n,2\pi n)$.
Функция $f\left(x\right)=cosx$ убывает при $x\in (2\pi n,\pi +2\pi n)$
Точки максимума $(2\pi n,1)$.
Точки минимума $(\pi +2\pi n,-1)$.
- Функция непрерывна на всей области определения.
Графиком функции $y=cosx$ является косинусоида (рис. 3).
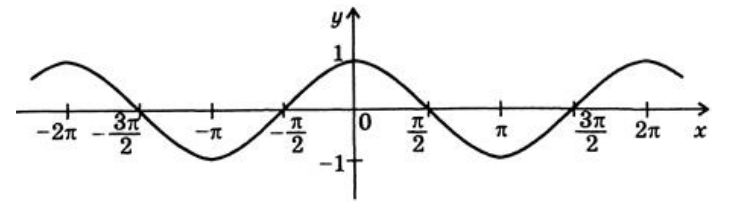
Рисунок 3. Косинусоида.
Свойства и график функции $f(x)=tgx$
- Область определения $x\in {\mathbb R}{\rm ,}{\rm \ }x\ne \frac{\pi }{2}+\pi n,\ n\in Z$.
- Область значения -- все числа.
- Функция нечетна.
- Функция периодическая с минимальным периодом $\pi $.
- При $x=0$, $y=0$. При $y=0$, $x=\pi n,n\in Z$.
- Функция выше оси $Ox$ при $x\in (\pi n,\frac{\pi }{2}+\pi n),n\in Z$.
- Функция ниже оси $Ox$ при $x\in (-\frac{\pi }{2}+\pi n,\frac{\pi }{2}+\pi n),n\in Z$.
- Функция возрастает на всей области определения.
- Функция непрерывна на всей области определения.
- ${\mathop{lim}_{x\to \frac{\pi }{2}+\pi n-0} tgx\ }=-\infty $, ${\mathop{lim}_{x\to \frac{\pi }{2}+\pi n+0} tgx\ }=+\infty $,
Графиком функции $y=tgx$ является тангенсоида (рис. 4).
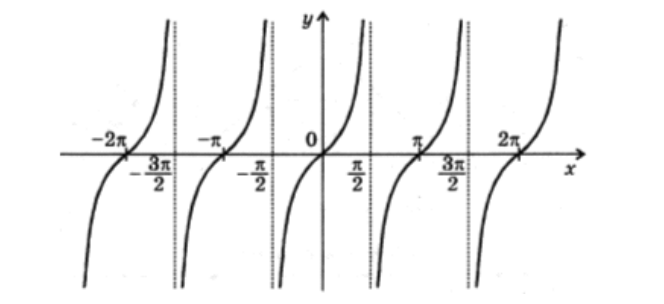
Рисунок 4. Тангенсоида.
Исследование свойств функции $y=ctgx$ мы предоставляем читателю.
Другие тригонометрические функции
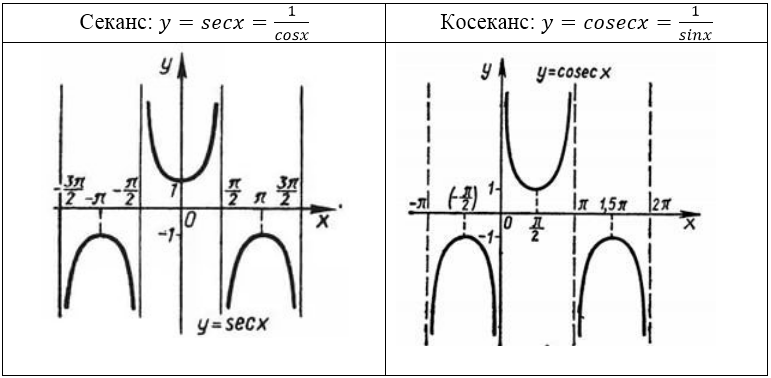
Рисунок 5.












