Понятие равнобедренного треугольника
Введем для начала определение треугольника.
Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда
Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.
Точки в рамках определения 1 называются вершинами треугольника.
Отрезки в рамках определения 1 называются сторонами треугольника.
Введем теперь понятие равнобедренного треугольника.
Треугольник будем называть равнобедренным, если две его стороны будут равны между собой.
Равные стороны в рамках определения 4, будем называть боковыми, а третью – основанием (рис. 1).
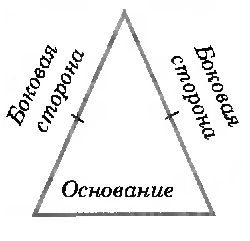
Отметим, что если боковые стороны равнобедренного треугольника также равняются его основанию, то треугольник будем называть равносторонним.
Свойства равнобедренного треугольника
Введем свойства равнобедренного треугольника в виде теорем.
Углы при основании равнобедренного треугольника будут равными.
Доказательство.
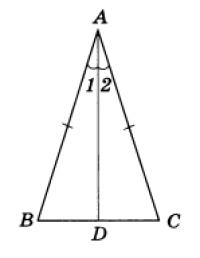
Пусть нам дан треугольник $ABC$, в котором $AB=AC$. Проведем биссектрису $AD$ к основанию данного нам треугольника (рис. 2).
Так как $AD$ – биссектриса, то будет верно равенство $∠1=∠2$
Для треугольников $ABD$ и $ACD$ сторона $AD$ является общей. Следовательно, треугольники $ABD$ и $ACD$ равны по первому признаку. Но тогда будет верно, что $∠B=∠C$
Теорема доказана.
Из этой теоремы можно выделить признак равнобедренности треугольника. Если в треугольнике будут иметься два равных угла, то он будет являться равнобедренным.
Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.
Доказательство.
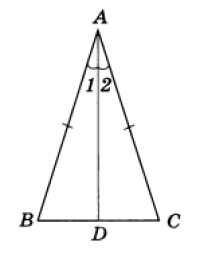
Пусть нам дан треугольник $ABC$, в котором $AB=AC$. Проведем биссектрису $AD$ к основанию данного нам треугольника (рис. 3). Докажем, для начала, что $AD$ является медианой.
Так как $AD$ – биссектриса, то будет верно равенство $∠1=∠2$
Для треугольников $ABD$ и $ACD$ сторона $AD$ является общей. Следовательно, треугольники $ABD$ и $ACD$ равны по первому признаку. Но тогда верно, что $BD=DC$. Следовательно, $AD$ – медиана.
Докажем теперь, что $AD$ - высота. Введем следующие обозначения. Пусть $∠1=α$, $∠B=β$.
Так как $AD$ – биссектриса, то $∠A=2α$.
По теореме о сумме углов в треугольнике, из треугольника $ABC$ будем иметь
$∠A+∠B+∠C=180^0$
То есть
$2α+2β=180^0$
$α+β=90^0$
Из треугольника $ABD$ будем иметь
$∠BDA+α+β=180^0$
Тогда
$∠BDA=180^0-(α+β)=180^0-90^0=90^0$
Следовательно, $AD$ - высота.
Теорема доказана.
Пример задач
Пусть дан треугольник $ABC$. Доказать, что если в нем $BD$ будет и высотой и медианой, то треугольник является равнобедренным.
Доказательство.
Для этого нам нужно доказать, что $AB=BC$.
Изобразим рисунок по условию задачи (рис. 4).
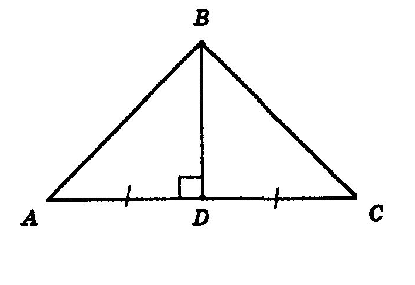
Так как $BD$ является медианой, то по определению 4 будет верно равенство
$AD=DC$
Так как $BD$ является высотой, то по определению 6 будет верно равенство
$∠ADB=∠BDC=90^0$
У треугольников $ADB$ и $BDC$ сторона $BD$ будет общей, следовательно, по всему сказанному выше эти треугольники равняются по первому признаку. Но тогда и стороны $AB$ и $BC$ равны.
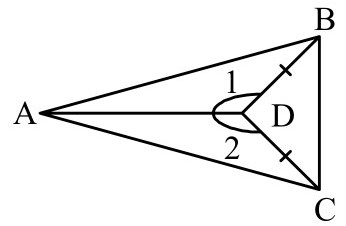
Пусть дан треугольник $ABC$. Доказать, что он будет равнобедренным в условиях рисунка 5.
Доказательство.
По условию задачи угол 1 равняется углу 2, а сторона $BD$ равняется стороне $CD$. Так как у треугольников $ADB$ и $ADC$ сторона $AD$ является общей, то треугольники $ADB$ и $ADC$ будут равняться по первому признаку. Но тогда и стороны $AB$ и $AC$ также равны между собой. Следовательно, данный треугольник будет равнобедренным.