
Равносильность уравнений
Если уравнения равносильны на множестве $M=M_{1} \bigcap M _{2} $, то будем говорить просто, что они Б-равносильны.
Пусть даны три уравнения: $f_{1} (x)=g_{1} (x)$(1) с областью определения $M_{1} $; $f_{2} (x)=g_{2} (x)$ (2) с областью определения $_{2} $; $f_{3} (x)=g_{3} (x)$с областью определения$_{3} $. И пусть $M\subseteq M_{1} \bigcap M_{2} \bigcap M_{3} $. Тогда, если уравнение (1) равносильно уравнению (2) на множестве $M$, уравнение (2) равносильно уравнению (3) на множестве $M$, то уравнение (1) равносильно уравнению (3) на множестве $A$.
Если одну или обе части данного уравнения тождественно преобразовать, то получим уравнение, Б-равносильное данному.
Если к обеим частям уравнения прибавить одно и то же математическое выражение, то получим уравнение, Б-равносильное данному.$(f(x)=g(x))\mathop{\Leftrightarrow }\limits^{} (f(x)+\varphi (x)=g(x)+\varphi (x))$
При этом область определения данного уравнения и нового совпадают.
Уравнения $f(x)=g(x)$(1) и $f(x)\varphi (x)=g(x)\varphi (x)$(2), где $\varphi (E)$не равно нулю в области определения уравнения (1), Б-равносильны.
Уравнение $f_{1} (x)f_{2} (x)...f_{n} (x)=0$(1) и совокупность уравнений
$\left[\begin{array}{l} {f_{1} (x)=0,} \\ {f_{2} (x)=0,} \\ {\cdots } \\ {f_{n} (x)=0} \end{array}\right. $ (2) Б-равносильны.
Уравнения $f(x)=g(x)$(1) и (2) $f^{2n+1} (x)=g^{2n+1} (x),$ где $n\in N$, Б-равносильны.
Уравнение $f^{n} (x)=g^{n} (x),$ где $n\in N$, является следствием уравнения$f(x)=g(x)$.
Уравнение $a^{f(x)} =a^{g(x)} $, где $a>0,a\ne 1$, Б-равносильно уравнению $f(x)=g(x)$
Уравнение $\log _{a} f(x)=\log _{a} g(x),$ где $a>0,a\ne 1$, Б-равносильно уравнению $f(x)=g(x)$.
Следствие 1. Уравнение $\log _{a} f(x)=\log _{a} g(x),$ где $a>0,a\ne 1$
Б-равносильно каждой из систем
$\left\{\begin{array}{l} {f(x)=g(x),} \\ {f(x)>0} \end{array}\right. $ и $\left\{\begin{array}{l} {f(x)=g(x),} \\ {g(x)>0.} \end{array}\right. $
Следствие 2. Уравнение $\log _{a} f(x)=b,$ где $a>0,a\ne 1$. Б-равносильно уравнению $f(x)=a^{b} $
Равносильность неравенств
Два неравенства, у первого з которых область определения $_{1} $, у другого $_{2} $, называются равносильными на множестве $\subseteq _{1} \bigcap _{2} $, если они имеют одни и те же решения или не имеют решений на этом множестве.
Если неравенства равносильны на множестве $M=M_{1} \bigcap M _{2} $, то будем говорить просто, что они Б-равносильны.
Пусть даны три неравенства: (1) с областью определения $M_{1} $; (2) с областью определения $M_{2} $; (3) с областью определения $M_{3} $. И пусть $M\subseteq M_{1} \bigcap M _{2} \bigcap M_{3} $. Тогда, если неравенство (1) равносильно неравенству (2) на множестве $M$, неравенство (2) равносильно неравенству (3) на множестве $M$, то неравенство (1) равносильно неравенству (3) на множестве $M$.
Если одну или обе части данного неравенства тождественно преобразовать, то получим неравенство, Б-равносильное данному.
Если к обеим частям неравенства прибавить одно и то же математическое выражение, то полученное неравенство того же смысла Б-равносильно данному.
Если обе части неравенства умножить на одно и то же выражение , принимающее в области определения данного неравенства только положительные (отрицательные) значения, то полученное неравенство того же (противоположного) смысла Б-равносильно данному.
Неравенство $f(x)\varphi (x) >0$ Б-равносильно совокупности двух систем
\[\left[\begin{array}{l} {\left\{\begin{array}{l} {f(x) >0,} \\ {\varphi (x) >0;} \end{array}\right. } \\ {\left\{\begin{array}{l} {f(x)Неравенство $f(x)\varphi (x) \[\left[\begin{array}{l} {\left\{\begin{array}{l} {f(x) >0,} \\ {\varphi (x)0.} \end{array}\right. } \end{array}\right. \]
Неравенство $f(x)\varphi (x)\ge 0$ Б-равносильно совокупности $\left[\begin{array}{l} {\left\{\begin{array}{l} {f(x)>0,} \\ {\varphi (x) >0,} \end{array}\right. } \\ {\left\{\begin{array}{l} {f(x)
Неравенство $f(x)\varphi (x)\le 0$ Б-равносильно совокупности $\left[\begin{array}{l} {\left\{\begin{array}{l} {f(x) >0,} \\ {\varphi (x)0,} \end{array}\right. } \\ {f(x)=0,} \\ {\varphi (x)=0.} \end{array}\right. $
Если обе части неравенства возвести в одну и ту же нечетную степень, то полученное неравенство того же смысла Б-равносильно данному.
Неравенство $f(x) >\varphi (x)$ (1) равносильно неравенству $f^{2n} (x) >\varphi ^{2n} (x)$ (2) на множестве решений системы неравенств
\[\left\{\begin{array}{l} {f(x)\ge 0,} \\ {\varphi (x)\ge 0.} \end{array}\right. \]Неравенство $a^{f(x)} >a^{\varphi (x)} $, где $a >0,a\ne 1$ Б-равносильно совокупности двух систем $\left[\begin{array}{l} {\left\{\begin{array}{l} {a >1,} \\ {f(x) >\varphi (x);} \end{array}\right. } \\ {\left\{\begin{array}{l} {0
Неравенство $f(x)^{g(x)} >f(x)^{h(x)} $Б-равносильно совокупности систем
\[\left[\begin{array}{l} {\left\{\begin{array}{l} {g(x) >h(x),} \\ {f(x) >1;} \end{array}\right. } \\ {\left\{\begin{array}{l} {g(x)Неравенство $\log _{a} f(x) >\log _{a} \varphi (x)$, где $a >0,a\ne 1$ Б-равносильно совокупности двух систем $\left[\begin{array}{l} {\left\{\begin{array}{l} {a>1,} \\ {f(x) >\varphi (x);} \end{array}\right. } \\ {\left\{\begin{array}{l} {0
Неравенство $\log _{g(x)} f(x) >\log _{g(x)} \varphi (x)$ (1) Б-равносильно совокупности систем $\left[\begin{array}{l} {\left\{\begin{array}{l} {g(x) >1,} \\ {f(x) >\varphi (x);} \end{array}\right. } \\ {\left\{\begin{array}{l} {0
Пример решения иррационального уравнения
Решить уравнение $\sqrt{2x-1}=x-2$
Найдем область определения:
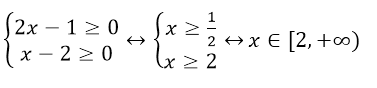
Рисунок 1.
Возведем обе части в квадрат:
\[2x-1=x^2-4x+4\] \[x^2-6x+5=0\] \[x=1-посторонний\ корень,\ x=5\]Ответ: $5$.











