Функция $f(x)=x^2$
Для начала вспомним определение квадратичной функции.
Функция вида $y=ax^2+bx+c$, где $a$ отлично от нуля, называется квадратичной функцией.
Функция $f\left(x\right)=x^2$ является частным случаем квадратичной функции, когда $a=1,\ b,c=0$. Графиком такой функции называется парабола.
Исследуем и построим график функции $f\left(x\right)=x^2$
- Область определения -- все числа.
- Так как квадрат любого числа всегда больше или равен нулю, то область значения $[0,\infty )$
- $f\left(-x\right)={(-x)}^2=x^2=f(x)$. Значит функция четна.
- При $x=0,\ y=0$ -0 функция проходит через начало координат.
- $f'\left(x\right)={\left(x^2\right)}'=2x$ \[2x=0,\] \[x=0\]
- $f^{''}\left(x\right)={\left(2x\right)}^{''}=2>0$.
- Для построения графика функции составим таблицу её значений:
- График функции -- парабола (рис. 1)
Методом интервалов, получим:
Функция возрастает при $x\in (0,+\infty )$
Функция убывает при $x\in (-\infty ,0)$
Следовательно, функция выпукла на всей области определения.
\[{\mathop{lim}_{x\to -\infty } x^2\ }=+\infty \] \[{\mathop{lim}_{x\to +\infty } x^2\ }=+\infty \]
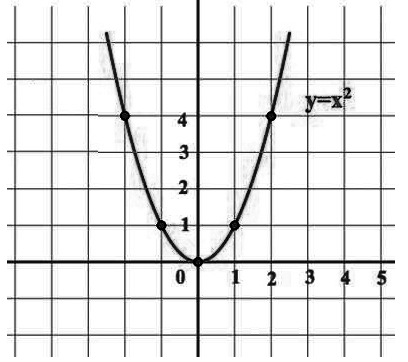
Рис. 1. Парабола $f\left(x\right)=x^2$.
Функция $f(x)=x^3$
Для начала вспомним определение кубической функции.
Функция вида $y=ax^3+bx^2+cx+d$, где $a$ отлично от нуля, называется кубической функцией.
Функция $f\left(x\right)=x^3$ является частным случаем кубической функции, когда $a=1,\ b,c=0$. Графиком такой функции называется кубическая парабола.
Исследуем и построим график функции $f\left(x\right)=x^3$
- Область определения -- все числа.
- Область значения -- все числа
- $f\left(-x\right)={(-x)}^3=-x^3=-f(x)$. Значит функция нечетна.
- При $x=0,\ y=0$ -0 функция проходит через начало координат.
- $f'\left(x\right)={\left(x^3\right)}'=3x^2$ \[3x^2=0,\] \[x=0\]
- $f^{''}\left(x\right)={\left(3x^2\right)}^{''}=6x$. \[6x=0\] \[x=0\]
- Для построения графика функции составим таблицу её значений:
- График функции -- кубическая парабола (рис. 2)
Так как квадрат любого числа всегда больше или равен нулю, то функция убывает на всей области определения.
Методом интервалов, получим:
Функция выпукла при $x\in (0,+\infty )$
Функция вогнута при $x\in (-\infty ,0)$
\[{\mathop{lim}_{x\to -\infty } x^2\ }=-\infty \] \[{\mathop{lim}_{x\to +\infty } x^2\ }=+\infty \]
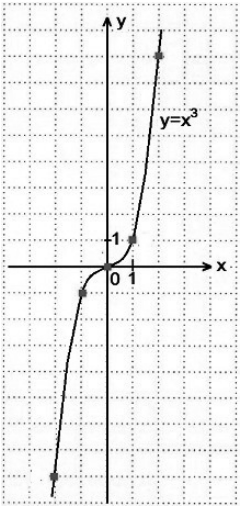
Рис. 2. Кубическая парабола $f\left(x\right)=x^3$.












