Оценки, надежность
Чаще всего оценки делятся на два вида: точечная оценка и интервальная оценка.
Точечная оценка -- оценка, которая определяется одним числом.
В математической статистике, при оценке различных совокупностей чаще сего используется интервальная оценка.
Интервальная оценка -- оценка, которая определяется двумя числами, которые являются концами интервала.
Для понятия интервальной оценки используются параметры точности и надежности оценки.
Точность оценки -- положительное число $\delta >0$, характеризующие величину расхождения между оценками выборки и генеральной совокупности, а именно:
\[\left|Q-Q^*\right|1.\]Надежность или доверительная вероятность оценки $Q\ по\ Q^*$ - вероятность $\gamma $, удовлетворяющее равенству:
\[P\left(Q^*-\deltaЧаще всего надежность имеет значения $0,95,\ 0,99\ и\ 0,999$, то есть значения, близкие к единице.
Доверительный интервал
Доверительный интервал -- интервал $(Q^*-\delta ,Q^*+\delta )$, который покрывает неизвестную величину $Q$ c надежностью $\gamma $, то есть $Q^*-\delta
Понятие доверительного интервала существует для оценки многих параметров выборки: математического ожидания, среднего квадратического отклонения, дисперсии
В данной статье мы не будем вдаваться в подробности вывода формул для нахождения доверительных интервалов.
- Доверительный интервал для оценки математического ожидания при заданном среднем квадратическом отклонении $\sigma $.
где $t$ находится из равенства $2Ф\left(t\right)=\gamma $.
- Доверительный интервал для оценки математического ожидания при неизвестном среднем квадратическом отклонении $\sigma $.
- Доверительный интервал для оценки среднего квадратического отклонения.
- Доверительный интервал для оценки дисперсии.
В последних двух пунктах $q$ имеет табличное значение (таблица 1).
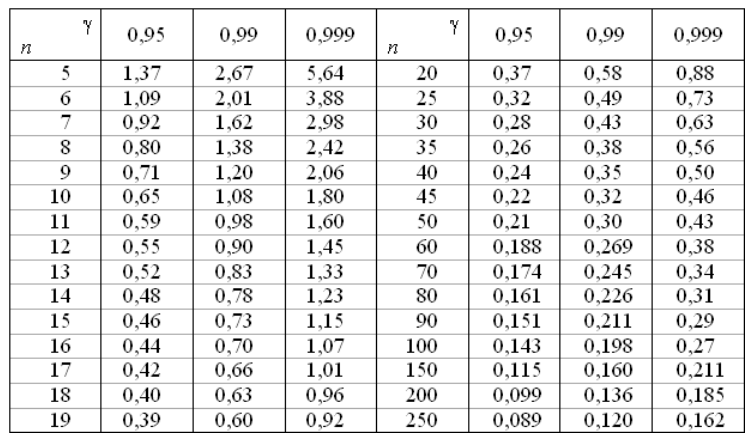
Рисунок 1. Значения величины $q$.
Пример задачи на нахождения доверительных интервалов
Пусть величина $X$ имеет нормальное распределение с дисперсией $\sigma =2$ и исправленным среднем квадратическим отклонением $S=1,8$. Пусть объем выборки $n=25$, а надежность равна $\gamma =0,99$.
Найти:1) доверительный интервал для оценки математического ожидания.
2) доверительный интервал для оценки среднего квадратического отклонения.
3) доверительный интервал для оценки дисперсии.
Решение:
1) Для нахождения доверительного интервала для оценки математического ожидания необходимо найти интервал вида
\[\left(\overline{x}-\frac{\sigma t}{\sqrt{n}};\overline{x}+\frac{\sigma t}{\sqrt{n}}\right)\]Параметр $t$ найдем из формулы
\[2Ф\left(t\right)=\gamma \]Откуда
\[Ф\left(t\right)=\frac{\gamma }{2}=\frac{0,99}{2}=0,495\]Из таблицы значений функции Лапласа получим, что $t=2,6$.
Имеем интервал:
\[\left(\overline{x}-\frac{4,6}{\sqrt{25}};\overline{x}+\frac{4,6}{\sqrt{25}}\right)=\left(\overline{x}-0,92;\overline{x}+0,92\right)\]2) Для начала найдем значение величины $q$. Так как $n=25$ и $\gamma =0,99$, то из таблицы 1, получим, что $q=0,49$.
Видим, что $q \[\left(S\left(1-q\right),S\left(1+q\right)\right)\] \[\left(1,8\cdot 0,51;1,8\cdot 1,49\right)=(0,918;2,682)\]
3) Так как, как было показано в пункте 2, $q \[\left(S^2\left(1-q\right),S^2\left(1+q\right)\right)\]
\end{enumerate}
Получим:
\[\left(1,6524;4,8276\right)\]










