Понятие окружности и круга
Перед тем, как ввести основные формулы для окружности и круга, введем, непосредственно понятия окружности и круга, и связанные с ними определения.
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Центром окружности будем называть точку, которая задается в рамках определения 1.
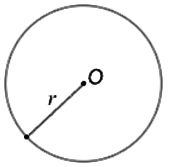
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки (Рис. 1).
Кругом будем называть часть плоскости, которая имеет своей границей окружность.
Длина окружности
Будем выводить длину произвольной окружности $C$ с помощью её радиуса, равного $τ$.
Будем рассматривать две произвольные окружности. Обозначим их длины через $C$ и $C'$, у которых радиусы равняются $τ$ и $τ'$. Будем вписывать в эти окружности правильные $n$-угольники, периметры которых равняются $ρ$ и $ρ'$, длины сторон которых равняются $α$ и $α'$, соответственно. Как мы знаем, сторона вписанного в окружность правильного $n$ – угольника равняется
$α=2τsin \frac{180^0}{n}$
Тогда, будем получать, что
$ρ=nα=2nτsin \frac{180^0}{n}$
$ρ'=nα'=2nτ'sin \frac{180^0}{n}$
Значит
$\frac{ρ}{ρ'}=\frac{2nτsin \frac{180^0}{n}}{2nτ'sin \frac{180^0}{n}}=\frac{2τ}{2τ'}$
Получаем, что отношение $\frac{ρ}{ρ'}=\frac{2τ}{2τ'}$ будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
$\lim_{n→∞}(\frac{ρ}{ρ'})=\frac{2τ}{2τ'}$
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть $n→∞$), будем получать равенство:
$\lim_{n→∞}(\frac{ρ}{ρ'})=\frac{C}{C'}$
Из последних двух равенств получим, что
$\frac{C}{C'}=\frac{2τ}{2τ'}$
То есть
$\frac{C}{2τ}=\frac{C'}{2τ'}$
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
$\frac{C}{2τ}=const$
Эту постоянную принять называть числом «пи» и обозначать $π$. Приближенно, это число будет равняться $3,14$ (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
$\frac{C}{2τ}=π$
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
$C=2πτ$
Площадь круга
Будем выводить площадь $S$ произвольного круга с помощью радиуса окружности, ограничивающей его, равного $τ$.
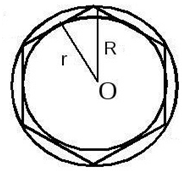
Впишем в такую окружность правильный $n$-угольник, площадь которого равняется $S_n$. В такой многоугольник впишем окружность, площадь которого равняется $S'_n$ (рис. 2).
Будет очевидна верность неравенства
$S >S_n >S'_n$
Используем формулу, которая связывает радиусы вписанной и описанной окружностей для правильного многоугольника:
$τ=Rcos \frac{180^0}{n}$
Если неограниченно увеличивать число сторон в таком правильном многоугольнике (то есть взять $n→∞$), то получим, что
$cos \frac{180^0}{n}→1$, $τ→R$
Тогда будет выполняться
$S→S'_n$, $S→S_n$
Также
$P_n→2πτ$
По формуле, площадь такого многоугольника равняется $S_n=\frac{1}{2} P_n τ$, следовательно
$S=S_n=\frac{1}{2}\cdot 2πτ\cdot τ=πτ^2$
То есть, для нахождения площади круга, нужно пользоваться формулой
$S=πτ^2$
Пример задачи
Найти длину окружности и площадь круга, который вписан в квадрат со стороной, равной $α$.
Решение.
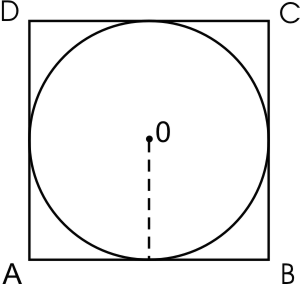
Пусть нам дан квадрат $ABCD$, в который вписана окружность с центром $O$. Изобразим рисунок по условию задачи (рис. 3).
Очевидно, что центр окружности будет совпадать с центром квадрата, в которой она вписана. Так как квадрат описан вокруг окружности, то его стороны будут касательными к ней, то есть радиус, проведенный, к примеру, к стороне $AB$ будет перпендикулярен к ней. Значит, диаметр окружности равняется стороне квадрата. То есть
$τ=\frac{α}{2}$
По формуле длины окружности, получим, что
$C=2π\cdot \frac{α}{2}=πα$
По формуле площади круга, получим, что
$S=π(\frac{α}{2})^2=\frac{πα}{4}$
Ответ: $C=πα$, $S=\frac{πα}{4}$.