Понятие движения
Введем для начала предварительные сведения о понятии движения.
Движением плоскости называется такое отображение плоскости на себя, при котором сохраняются расстояния.
Приведем несколько теорем на понятие движения (в этой статье мы не будем рассматривать их доказательства).
При движении треугольник отображается на равный ему треугольник.
Любое движение является наложением.
При движении любая фигура отображается на равную ей фигуру.
Далее рассмотрим примеры движений в планиметрии.
Осевая симметрия
Понятие осевой симметрии связано с симметричностью относительно какой-либо прямой.
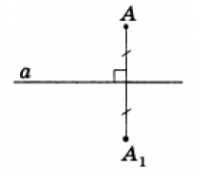
Точки $A$ и $A_1$ называются симметричными относительно прямой $a$, если эта прямая перпендикулярна к отрезку ${AA}_1$ и проходит через его центр (рис. 1).
 Осевая симметрия">
Осевая симметрия">
Рисунок 1. Осевая симметрия
Рассмотрим пример построения осевой симметрии.
Построить осевую симметрию треугольника $ABC$ относительно стороны $BC$.
Решение.
Из определения, очевидно, что при такой осевой симметрии сторона $BC$ перейдет в саму себя. Точка $A$ перейдет в точку $A_1$ такую, что ${AA}_1\bot BC$, ${AH=HA}_1$. Получаем, что треугольник $ABC$ переходит в треугольник $A_1BC$ (Рис. 2).
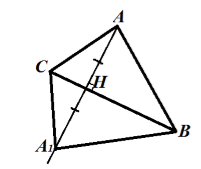
Рисунок 2.
С понятием осевой симметрии также связано понятие фигуры, обладающей осевой симметрией.
Фигура называется симметричной относительно прямой $a$, если каждая симметричная точка этой фигуры принадлежит этой же фигуре (рис. 3).
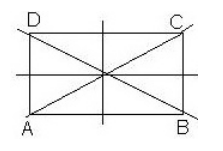
Рисунок 3. Пример фигуры, обладающей осевой симметрией
Центральная симметрия
Понятие центральной симметрии связано с симметричностью относительно какой-либо точки.
Точки $X$ и $X_1$ называются симметричными относительно точки $O$, если точка $O$ является центром отрезка ${XX}_1$ (рис. 4).
 Центральная симметрия">
Центральная симметрия">
Рисунок 4. Центральная симметрия
Рассмотрим пример построения центральной симметрии.
Построить центральную симметрию треугольника $ABC$ относительно вершины $A$.
Решение.
Из определения, очевидно, что при такой центральной симметрии вершина $A$ перейдет в саму себя. Точка $B$ перейдет в точку $B_1$ такую, что ${BA=AB}_1$, а точка $C$ перейдет в точку $C_1$ такую, что ${CA=AC}_1$. Получаем, что треугольник $ABC$ переходит в треугольник ${AB}_1C_1$ (Рис. 5).
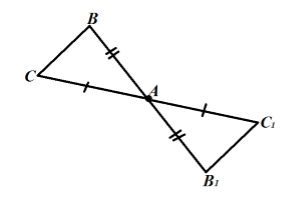
Рисунок 5.
С понятием центральной симметрии также связано понятие фигуры, обладающей центральной симметрией.
Фигура является симметричной относительно точки $O$, если каждая симметричная точка этой фигуры принадлежит этой же фигуре (рис. 6).
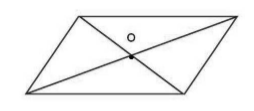
Рисунок 6. Пример фигуры, обладающей центральной симметрией
Параллельный перенос
Параллельный перенос на вектор $\overrightarrow{a}$ - отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что $\overrightarrow{{MM}_1}=\overrightarrow{a}$ (Рис. 7).
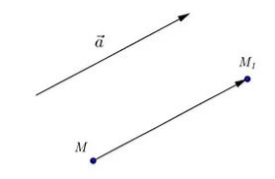
Рисунок 7. Параллельный перенос
Построить параллельный перенос треугольника $ABC$ на вектор $\overrightarrow{BC}$.
Решение.
Перенесем каждую вершину треугольника на вектор $\overrightarrow{BC}$. Получаем треугольник $CA_1C_1$ (рис. 8).
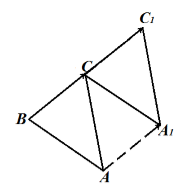
Рисунок 8.
Поворот
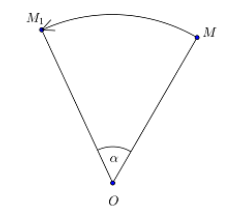
Поворотом вокруг точки $O$ на угол $\alpha $ называется такое движение плоскости, при котором любая точка $M$ отображается на точку $M_1$ такую, что ${OM}_1=OM,\ \angle M{OM}_1=\angle \alpha $ (Рис. 9).
 Поворот">
Поворот">
Рисунок 9. Поворот











