Напомним для начала определение решения системы линейных уравнений с двумя переменными.
Пара чисел называется решением линейного уравнения с двумя переменными, если при их подстановки в уравнение получается верное равенство.
В дальнейшем будем рассматривать системы из двух линейных уравнений с двумя переменными.
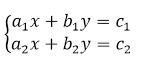
Рисунок 1.
Существуют три способа решения систем линейных уравнений: способ подстановки, способ сложения и графический способ. Рассмотрим его на следующем примере:
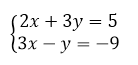
Рисунок 2.
Способ подстановки
Способ подстановки заключается в следующем: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
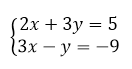
Рисунок 3.
Выразим из второго уравнения $y$ через $x$:
Подставим в первое уравнение, найдем $x$:
Найдем $y$:
Ответ: $(-2,\ 3)$
Способ сложения
Рассмотрим данный способ на примере:
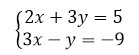
Рисунок 4.
Умножим второе уравнение на $3$, получим:
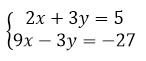
Рисунок 5.
Теперь сложим оба уравнения между собой:
Найдем $y$ из второго уравнения:
Ответ: $(-2,\ 3)$
!!! Отметим, что в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении одна из переменных «исчезла».
Графический способ
Графический способ заключается в следующем: Оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
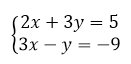
Рисунок 6.
Выразим из обоих уравнений $y$ через $x$:
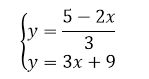
Рисунок 7.
Изобразим оба графика на одной плоскости:
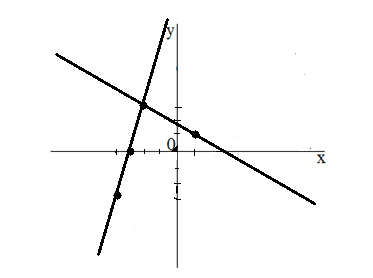
Рисунок 8.
Ответ: $(-2,\ 3)$
Пример решения систем линейных уравнений с двумя переменными
Решить систему уравнений тремя способами:
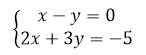
Рисунок 9.
Решение:
1) Способ подстановки.
Выразим $x$ через $y$:
\[x=y\]Подставим в второе уравнение, найдем $y$:
\[2y+3y=-5\] \[y=-1\]Найдем $x$:
\[x=-1\]Ответ: $(-1,-1)$
2) Способ сложения.
Умножим первое уравнение на $3$, получим:
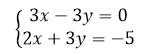
Рисунок 10.
сложим оба уравнения между собой:
\[5x=-5\] \[x=-1\]Найдем $y$ из первого уравнения:
\[-1-y=0\] \[y=-1\]Ответ: $(-1,\ -1)$
3) Графический способ.
Выразим из обоих уравнений $y$ через $x$:
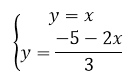
Рисунок 11.
Изобразим оба графика на одной плоскости:
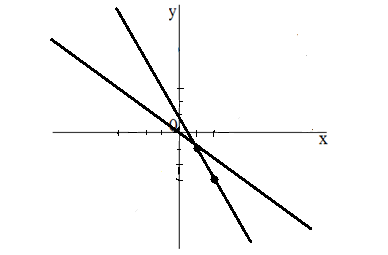
Рисунок 12.
Ответ: $(-1,\ -1)$












