Пусть дана двумерная случайная величина $(X,Y)$.
Законом распределения двумерной случайной величины $(X,Y)$ - называется множество возможных пар чисел $(x_i,\ y_j)$ (где $x_i \epsilon X,\ y_j \epsilon Y$) и их вероятностей $p_{ij}$.
Чаще всего закон распределения двумерной случайной величины записывается в виде таблицы (Таблица 1).
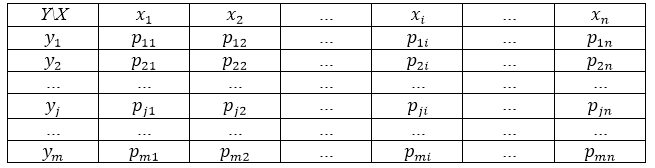
Рисунок 1. Закон распределения двумерной случайной величины.
Вспомним теперь теорему о сложении вероятностей независимых событий.
Вероятность суммы конечного числа независимых событий ${\ A}_1$, ${\ A}_2$, ... ,$\ {\ A}_n$ вычисляется по формуле:
\[P\left(\sum\limits^n_{i=1}{{\ A}_n}\right)=\sum\limits^n_{i=1}{P({\ A}_n)}\]Пользуясь этой формулой можно получить законы распределения для каждой компоненты двумерной случайной величины, то есть:
Отсюда будет следовать, что сумма всех вероятностей двумерной системы имеет следующий вид:
Рассмотрим подробно (поэтапно) задачу, связанную с понятием закона распределения двумерной случайной величины.
Закон распределения двумерной случайной величины задан следующей таблицей:

Рисунок 2.
Найти законы распределения случайных величин $X,\ Y$, $X+Y$ и проверить в каждом случае выполнение равенства полной суммы вероятностей единице.
- Найдем сначала распределение случайной величины $X$. Случайная величина $X$ может принимать значения $x_1=2,$ $x_2=3$, $x_3=5$. Для нахождения распределения будем пользоваться теоремой 1.
Найдем вначале сумму вероятностей $x_1$ следующим образом:
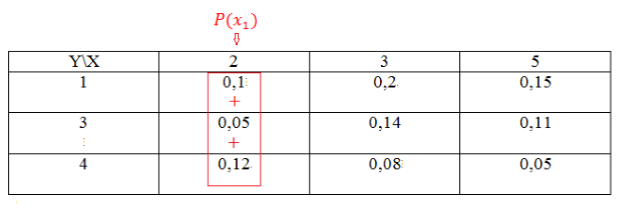
Рисунок 3.
Аналогично найдем $P\left(x_2\right)$ и $P\left(x_3\right)$:
\[P\left(x_2\right)=0,2+0,14+0,08=0,42\] \[P\left(x_3\right)=0,15+0,11+0,05=0,31\]Значит, закон распределения величины $X$ имеет следующий вид:

Рисунок 4.
Проверим выполнение равенства полной суммы вероятностей:
\[0,27+0,42+0,31=1-верно.\]- Найдем теперь распределение случайной величины $Y$. Случайная величина $Y$ может принимать значения $x_1=1,$ $x_2=3$, $x_3=4$. Для нахождения распределения будем пользоваться теоремой 1.
Найдем вначале сумму вероятностей $y_1$ следующим образом:
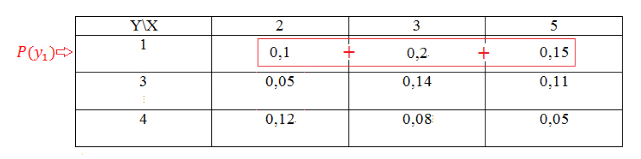
Рисунок 5.
Аналогично найдем $P\left(y_2\right)$ и $P\left(y_3\right)$:
\[P\left(y_2\right)=0,05+0,14+0,11=0,3\] \[P\left(y_3\right)=0,12+0,08+0,05=0,25\]Значит, закон распределения величины $X$ имеет следующий вид:

Рисунок 6.
Проверим выполнение равенства полной суммы вероятностей:
\[0,45+0,3+0,25=1-верно.\]- Осталось найти закон распределения случайной величины $X+Y$.
Обозначим её для удобства через $Z$: $Z=X+Y$.
Вначале найдем, какие значения может принимать данная величина. Для этого будем попарно складывать значения величин $X$ и $Y$. Получим следующие значения: 3, 4, 6, 5, 6, 8, 6, 7, 9. Теперь, отбрасывая совпавшие величины, получим, что случайная величина $X+Y$ может принимать значения $z_1=3,\ z_2=4,\ z_3=5,\ z_4=6,\ z_5=7,\ z_6=8,\ z_7=9.\ $
Найдем для начала $P(z_1)$. Так как значение $z_1$ единично, то оно находится следующим образом:
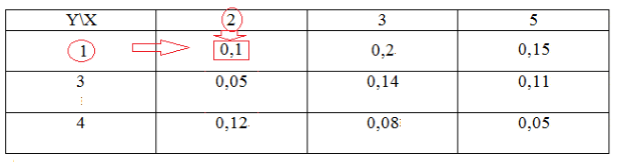
Рисунок 7.
Аналогично находятся се вероятности, кроме $P(z_4)$:
\[P\left(z_2\right)=0,2,\ P\left(z_3\right)=0,05,\ P\left(z_5\right)=0,08,\ P\left(z_6\right)=0,11,\ P\left(z_7\right)=0,05\]Найдем теперь $P(z_4)$ следующим образом:
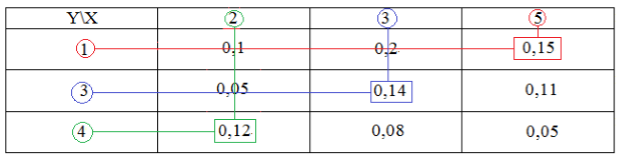
Рисунок 8.
Значит, закон распределения величины $Z$ имеет следующий вид:

Рисунок 9.
Проверим выполнение равенства полной суммы вероятностей:
\[0,1+0,2+0,05+0,41+0,08+0,11+0,05=1-верно.\]











