При решении разного рода неравенств удобным способом их решения является приведение их к виду квадратного неравенства.
Иррациональные неравенства
Неравенства, в которых функции находятся под знаком корня, называют иррациональными.
Иррациональные неравенства решаются путем возведения его левой и правой части в необходимую степень. Например, если в неравенстве используются квадратные корни, то обе его части возводят в квадрат, если используются кубические корни, то в куб и т.д.
Заметим, что возвести во вторую степень обе части неравенства без нарушения равносильности возможно лишь в том случае, когда они неотрицательные. В других случаях не всегда можно получить равносильное неравенство.
Например, имеем верное неравенство $-11
Рассмотрим правила получения равносильных систем для наиболее распространенных типов неравенств.
Неравенство вида $\sqrt{f_1(x)}
Замечание 2
При возведении во вторую степень обеих частей неравенства $\sqrt{f_1(x)}
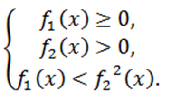
Пример 1
Найти решение иррационального неравенства $\sqrt{x^2-11x}
Решение.
Составим равносильную систему:
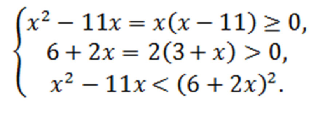
Решение неравенства $x(x-11) \ge 0$: $x \in (-\infty;0] \cup [11; +\infty)$.
Из второго неравенства получаем $x > -3$.
Третье неравенство системы дает результат $3x^2+35x+36 > 0$. Отсюда получаем решение $x \in (-\infty;-10,5) \cup (-1,1; +\infty)$.
Составляем систему из трех полученных решений неравенств:
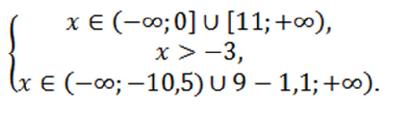
Решением системы будет $x \in [-1,1;0] \cup [11; +\infty)$.
Ответ: $x \in [-1,1;0] \cup [11; +\infty)$.
Неравенство вида $\sqrt{f_1(x)} > f_2(x)$
Замечание 3
При возведении во вторую степень обеих частей неравенства $\sqrt{f_1(x)} > f_2(x)$ его равносильность не нарушится при выполнении совокупности условий:
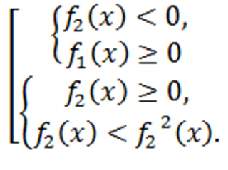
Пример 2
Найти решение иррационального неравенства $\sqrt{x+3} \ge 3+4x$.
Решение.
Воспользуемся совокупностью для решения данного неравенства.
Запишем первую систему неравенств:
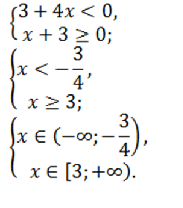
Данная система решений не имеет.
Запишем вторую систему неравенств:
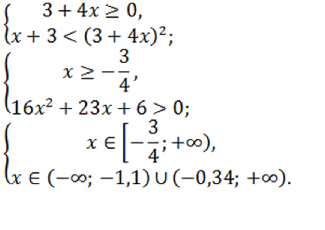
Решением данной системы является $x \in [-0,34; +\infty)$.
Найдем решение совокупности, т.е. объединим результаты 1 и 2 пунктов:
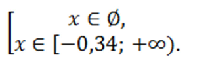
Ответ: $x \in [-0,34; +\infty)$.
Неравенство вида $\sqrt{f_1(x)} \le \sqrt{f_2(x)}$
Замечание 4
При возведении во вторую степень обеих частей неравенства $\sqrt{f_1(x)} \le \sqrt{f_2(x)}$ его равносильность не нарушится при выполнении следующих условий:
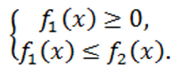
Пример 3
Найти решение иррационального неравенства $\sqrt{x^2-3x+2} \le \sqrt{8-3x}$.
Решение.
Воспользуемся правилом решения данного вида неравенств и составим равносильную систему:
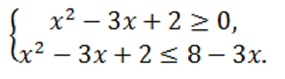
Решив первое неравенство, получим:
$x \in (-\infty; 1] \cup [2; +\infty)$.
Решив второе неравенство системы, получим:
$x^2-6 \le 0$;
$x \in [-\sqrt{6}; \sqrt{6}]$.
Найдем решение всей системы и решим систему из полученных результатов:
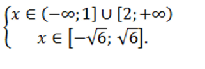
Очевидно, что решением данной системы являются общие решения двух уравнений системы, т.е. $x \in [-\sqrt{6}; 1] \cup [2; \sqrt{6}]$.
Ответ: $x \in [-\sqrt{6}; 1] \cup [2; \sqrt{6}]$.
Неравенство вида $\frac{\sqrt{f_1(x)}-f_2(x)}{g(x)} \le 0 ( \ge 0)$
Замечание 5
При возведении во вторую степень обеих частей неравенства $\frac{\sqrt{f_1(x)}-f_2(x)}{g(x)} \le 0 ( \ge 0)$ его равносильность не нарушится при выполнении следующих условий:
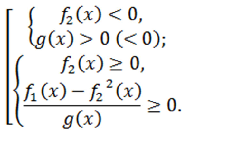
Логарифмические неравенства
Замечание 6
Логарифмические неравенства сводятся к решению квадратных неравенств путем перехода к решению неравенств относительно логарифмов к неравенствам для подлогарифмических функций.
При возведении во вторую степень обеих частей неравенства $\sqrt{f_1(x)}
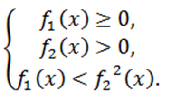
Найти решение иррационального неравенства $\sqrt{x^2-11x}
Решение.
Составим равносильную систему:
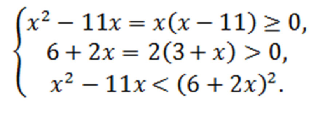
Решение неравенства $x(x-11) \ge 0$: $x \in (-\infty;0] \cup [11; +\infty)$.
Из второго неравенства получаем $x > -3$.
Третье неравенство системы дает результат $3x^2+35x+36 > 0$. Отсюда получаем решение $x \in (-\infty;-10,5) \cup (-1,1; +\infty)$.
Составляем систему из трех полученных решений неравенств:
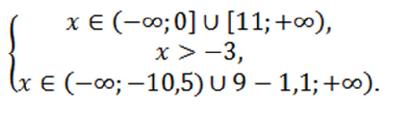
Решением системы будет $x \in [-1,1;0] \cup [11; +\infty)$. Ответ: $x \in [-1,1;0] \cup [11; +\infty)$.
При возведении во вторую степень обеих частей неравенства $\sqrt{f_1(x)} > f_2(x)$ его равносильность не нарушится при выполнении совокупности условий:
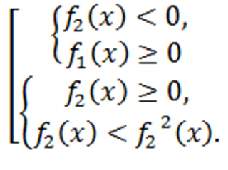
Найти решение иррационального неравенства $\sqrt{x+3} \ge 3+4x$.
Решение.
Воспользуемся совокупностью для решения данного неравенства.
Запишем первую систему неравенств:
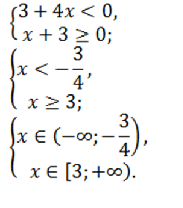
Данная система решений не имеет. Запишем вторую систему неравенств:
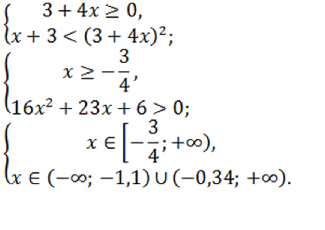
Решением данной системы является $x \in [-0,34; +\infty)$.
Найдем решение совокупности, т.е. объединим результаты 1 и 2 пунктов:
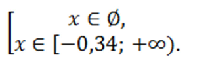
Ответ: $x \in [-0,34; +\infty)$.
При возведении во вторую степень обеих частей неравенства $\sqrt{f_1(x)} \le \sqrt{f_2(x)}$ его равносильность не нарушится при выполнении следующих условий:
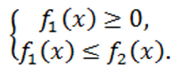
Найти решение иррационального неравенства $\sqrt{x^2-3x+2} \le \sqrt{8-3x}$.
Решение.
Воспользуемся правилом решения данного вида неравенств и составим равносильную систему:
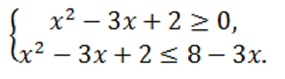
Решив первое неравенство, получим:
$x \in (-\infty; 1] \cup [2; +\infty)$.
Решив второе неравенство системы, получим:
$x^2-6 \le 0$;
$x \in [-\sqrt{6}; \sqrt{6}]$.
Найдем решение всей системы и решим систему из полученных результатов:
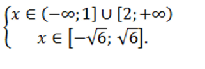
Очевидно, что решением данной системы являются общие решения двух уравнений системы, т.е. $x \in [-\sqrt{6}; 1] \cup [2; \sqrt{6}]$.
Ответ: $x \in [-\sqrt{6}; 1] \cup [2; \sqrt{6}]$.
При возведении во вторую степень обеих частей неравенства $\frac{\sqrt{f_1(x)}-f_2(x)}{g(x)} \le 0 ( \ge 0)$ его равносильность не нарушится при выполнении следующих условий:
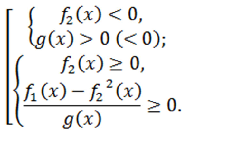
Логарифмические неравенства сводятся к решению квадратных неравенств путем перехода к решению неравенств относительно логарифмов к неравенствам для подлогарифмических функций.
Рассмотрим на примере алгоритм решения.
Найти решение неравенства $\log_4 {1-4x+3x^2} \le 5$.
Решение.
-
Найдем ОДЗ функции:
$1-4x+3x^2 > 0$;
$(x-\frac{1}{3})(x-1) > 0$;
$x \in (-\infty; \frac{1}{3}) \cup (1; +\infty)$.
-
Запишем правую часть неравенства в виде логарифма с основанием 4:
$\log_4 {1-4x+3x^2} \le \log_4 {4^5}$.
-
Переходим к решению неравенства относительно подлогарифмических функций. Т.к. основание логарифма $> 1$, то знак неравенства остается прежним:
$1-4x+3x^2 \le 4^5$,
$3x^2-4x-1023 \le 0$;
$(x-1,5+\frac{\sqrt{3073}}{3})(x-1,5-\frac{\sqrt{3073}}{3}) \le 0$.
Функция $f(x)=3x^2-4x-1023$ – парабола с ветками, направленными вверх, поэтому решением данного неравенства будет $x \in [1,5-\frac{\sqrt{3073}}{3};1,5+\frac{\sqrt{3073}}{3}]$.
-
Для нахождения решения логарифмического уравнения решим систему из уравнения ОДЗ и найденного решения неравенства из подлогарифмических функций:
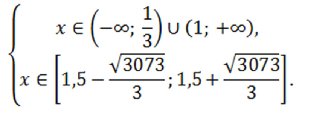
Решением системы, а значит и логарифмического уравнения, является $x \in [1,5-\frac{\sqrt{3073}}{3}; \frac{1}{3}) \cup (1; 1,5+\frac{\sqrt{3073}}{3}]$.
Ответ: $x \in [1,5-\frac{\sqrt{3073}}{3}; \frac{1}{3}) \cup (1; 1,5+\frac{\sqrt{3073}}{3}]$.












