Для выяснения геометрического значения производной рассмотрим график функции y = f(x). Возьмем произвольную точку М с координатами (x, y) и близкую к ней точку N (x + $\Delta $x, y + $\Delta $y). Проведем ординаты $\overline{M_{1} M}$ и $\overline{N_{1} N}$, а из точки М -- параллельную оси ОХ прямую.
Получим:
Отношение $\frac{\Delta y}{\Delta x} $ является тангенсом угла $\alpha $1, образованного секущей MN с положительным направлением оси ОХ. При стремлении $\Delta $х к нулю точка N будет приближаться к M, а предельным положением секущей MN станет касательная MT к кривой в точке M. Таким образом, производная f`(x) равна тангенсу угла $\alpha $, образованного касательной к кривой в точке M (х, y) с положительным направлением к оси ОХ -- угловому коэффициенту касательной (рис.1).
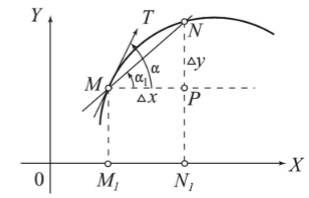
Рисунок 1. График функции
Вычисляя значения по формулам (1), важно не ошибиться в знаках, т.к. приращение может быть и отрицательным.
Точка N, лежащая на кривой, может стремиться к M с любой стороны. Так, если на рисунке 1, касательной придать противоположное направление, угол $\alpha $ изменится на величину $\pi $, что существенно повлияет на тангенс угла и соответственно угловой коэффициент.
Следует вывод, что существование производной связано с существованием касательной к кривой y = f(x), а угловой коэффициент -- tg $\alpha $ = f`(x) конечный. Поэтому касательная не должна быть параллельной оси OY, иначе $\alpha $ = $\pi $/2, а тангенс угла будет бесконечным.
В некоторых точках непрерывная кривая может не иметь касательной или иметь касательную параллельную оси OY (рис.2). Тогда в этих значениях функция не может иметь производную. Подобных точек может быть сколько угодно много на кривой функции.
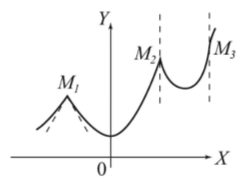
Рисунок 2. Исключительные точки кривой
Рассмотрим рисунок 2. Пусть $\Delta $x стремится к нулю со стороны отрицательных или положительных значений:
\[\Delta x\to -0\begin{array}{cc} {} & {\Delta x\to +0} \end{array}\]Если в данном случае отношения (1) имеют конечный придел, он обозначается как:
\[f`(x-0)\begin{array}{cc} {} & {f`(x+0)} \end{array}\]В первом случае -- производная слева, во втором -- производная справа.
Существование предела говорит о равносильности и равенстве левой и правой производной:
\[f`(x)=f`(x-0)=f`(x+0)\]Если же левая и правая производные неравны, то в данной точке существуют касательные не параллельные OY (точка М1, рис.2). В точках М2, М3 отношения (1) стремятся к бесконечности.
Для точек N лежащих слева от M2, $\Delta $x $
Справа от $M_2$, $\Delta $x $>$ 0, но выражение также f(x + $\Delta $x) -- f(x) $
Для точки $M_3$ слева $\Delta $x $$ 0 и f(x + $\Delta $x) -- f(x) $>$ 0, т.е. выражения (1) и слева, и справа положительны и стремятся к +$\infty $ как при приближении $\Delta $x к -0, так и к +0.
Случай отсутствия производной в конкретных точках прямой (x = c) представлен на рисунке 3.
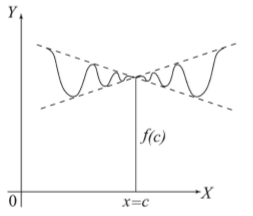
Рисунок 3. Отсутствие производных
На рисунке 4 изображен график функции и касательной к графику в точке с абсциссой $x_0$. Найти значение производной функции в абсциссе.
Решение. Производная в точке равна отношению~приращения функции к приращению аргумента. Выберем на касательной две точки с целочисленными координатами. Пусть, например, это будут точки F (-3,2) и C (-2.4).
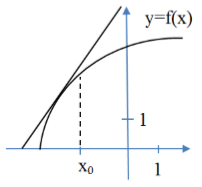
Рисунок 4. График функции
Найдем приращение аргумента:
$\Delta $x = х2 -- х1 = -2 -- (-3) = 1
Найдем приращение функции:
$\Delta$ y = y2 -- y1 = 4 -- 2 = 2
Тогда значение производной:
\[\frac{\Delta y}{\Delta x} =\frac{2}{1} =2\]На рисунке 5 изображен график функции. Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите значение производной функции в точке $x_0$=8.
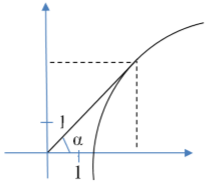
Рисунок 5. График функции
Решение.
Обозначим границы треугольника точками О, А, В (рисунок 6). И найдем тангенс угла $\alpha $.
\[tg\alpha =tgAOB=\frac{AB}{OB} =\frac{10}{8} =1,25\]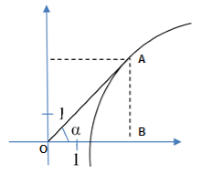
Рисунок 6. Нахождение производной












